मीराचं शिक्षण नुकतंच पूर्ण झालं होतं. ऑस्ट्रेलियाला जाऊन MS केलं आणि तिकडेच पुढे PhD देखील करण्याची तिची इच्छा होती. पण आई-वडिलांच्या मते वय वाढत चालल्याने आता तिच्या लग्नाचं बघायला सुरुवात करणं आवश्यक होतं. 'तुझं कुठं काही आहे का? आत्ताच सांग बाई! नंतर अभ्रूचे धिंडवडे नकोत आमच्या.' असं तिच्या वडिलांनी विचारल्यावर तिचं कोणावरही प्रेम नाही किंवा तिच्या मनात देखील कोणी नाही असे सांगताच 'आम्ही आता तुझ्यासाठी स्थळ बघायला मोकळे, हो की नाही?' असे तिच्या वडिलांनी विचारले. जरा नाराज होऊनच तिने 'हो' म्हणून सांगितले. तिला पुढे अजून शिकायचं होतं. अगदी परदेशातच नाही तर भारतात सुद्धा तिला चाललं असतं.
गणित कसे शिकवावे ह्यावर बोलण्याची माझी काही फार पात्रता नाही. मी शिक्षणतज्ज्ञ आहे अशातला भाग नाही. परंतु एक गणितज्ञ ह्या नात्याने मुलांना त्यांच्या शालेय वयातील शिक्षणातून कोणते ज्ञान मिळावे जेणेकरून त्यांची गणितातील प्रतिभा वाढीस लागेल, ह्याचे काही आडाखे माझ्या मनात आहेत. तसेच माझे स्वतःचे काही अनुभवसुद्धा आहेत. ह्या सर्वांची सरमिसळ म्हणजे हा लेख.
उपयोग काय?
मी भारत सोडला आणि सर्वप्रथम एक वर्ष ऑस्ट्रेलियामध्ये राहिले. त्यानंतर स्कॉटलंडला आले आणि येथलीच झाले. ह्या दोन्ही देशांत विद्यापीठांमध्ये संशोधन सहाय्यक म्हणून काम केले आणि मोठा अलिबाबाचा खजिना असल्यासारखे संशोधनाचे विश्व माझ्यापुढे खुले झाले. आयुष्यात करण्यासारखे आणि शिकण्यासारखे कितीतरी आहे हे कळले. आपले ज्ञान किती खुजे आहे आणि नवीन ज्ञान मिळविण्यात आणि संशोधन करण्यामध्ये कितीतरी आत्मिक आनंद आहे हे जाणवले . हा आत्मिक आनंद अधिकाधिक मिळविता यावा म्हणून संशोधनात पदवी (डॉक्टरेट) घेण्याचे ठरविले. शिष्यवृत्तीसकट मला पीएच. डी. ला प्रवेश मिळाला आणि माझा एक सुंदर प्रवास सुरु झाला. पीएच.
उपोद्घात
पायथागोरसच्या प्रमेयाबद्दल ऐकले नसेल, असे सहसा होत नाही. जवळपास प्रत्येकाने लहानपणी
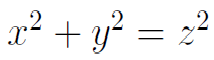
हे समीकरण पाहिलेले आहे. पायथागोरसची त्रिकूटे म्हणजे ह्या समीकरणाच्या अशा उकली, ज्यामध्ये प्रत्येक x, y, z पूर्णांक आहेत. उदा. (३, ४, ५) , (५, १२, १३) , (८, १५, १७) , (६, ८, १०) इ. ह्यांबद्दल सुद्धा आपण ऐकले असेल. अशी किती त्रिकूटे आहेत? सगळी सांगता येतील का? असा प्रश्न विचारता येऊ शकतो. आज आपण ह्याच प्रश्नाकडे बघू.
प्राथमिक माहिती
अशा विषयावर लिहिताना आड्यन्ससाठी सुरवात हलकीफुलकी करावी असा संकेत आहे. पुण्यात (मायबोलीवर?) सुद्धा जर लोकांना थोडे हसवले नाही तर तो फाऊल धरतात असे ऐकले आहे. ह्या नियमाला जागून -
An Experimental Physicist and a Mathematician meet each other. The Physicist asked the Mathematician - "What area do you study?" He answered - "Knot Theory." Physicist replied - "Me neither!"
याआधीचे लिखाण येथे - http://www.maayboli.com/node/41358
गणितातल्या समजावयास सोप्या प्रश्नांवर लेख लिहावयाचे बर्याच दिवसांपासून मनात आहे. पुढील लिखाण हे थोडेसे prelude म्हणून आहे. ह्यात तांत्रिक माहिती अशी नाही. 'तुम्ही काय करता हो?' ह्या प्रश्नाचे अत्यंत ढोबळ उत्तर. पुढे सवड होईल तसे जास्त specific लेख लिहीन किंवा ह्याच लेखाला पुरवण्या जोडत जाईन.
ह्या ग्रूपचे नाव 'संशोधन पूर्ण झालेले मायबोलीकर' असे नसून 'संशोधनक्षेत्रातील मायबोलीकर' असे आहे. त्यामुळेच येथे लिहिण्याची जुर्रत करतो. {ग्रूप निर्मात्याचे/ निर्मातीचे आभार मानून.  } मी अमूर्त गणितात सध्या पीएचडी करत आहे. आज जरा गणिताविषयी लिहीन. पुढे कधीतरी मी स्वतः काय करतो याबद्दल माहिती देईन.
} मी अमूर्त गणितात सध्या पीएचडी करत आहे. आज जरा गणिताविषयी लिहीन. पुढे कधीतरी मी स्वतः काय करतो याबद्दल माहिती देईन.
टीप : येथून पुढे मी 'अमूर्त गणित' आणि 'गणित' हे शब्द बहुतांशी समान अर्थाने वापरेन.
गणित म्हणजे काय?
प्रकरण २.
कोणत्याही संख्येला ११ च्या पटीतील संख्येने गुणणे.
उदाहरण १. ३ ४ ७ × २ २
३ ४ ७ × २ २ = ३ ४ ७ × २ × ११.
३ ४ ७ × २ = ६९४. हे अगदी सोपे आहे.
ते ३।४७ × २ = ६।९४ असे करता येईल. जर उजव्या बाजूला हातचा असेल तर तो डावीकडच्या भागात मिळवावा लागेल.
आता ६९४ × ११ = ७६३४. हा गुणाकार तोंडी करायला आपण शिकलो आहोतच.
म्हणून ३ ४ ७ × २ २ = ७६३४.
उदाहरण २. ४ ५ ९ × ३ ३
४ ५ ९ × ३ ३ = ४ ५ ९ × ३ × ११.
४ ५ ९ × ३ = १ ३ ७ ७. हेही अगदी सोपे आहे.
आता १३७७ × ११ = १५१४७.
म्हणून ४ ५ ९ × ३ ३ = १५१४७.
याचप्रमाणे ४४, ५५ इत्यादी संख्यांनीही गुणता येईल.
उदाहरण ३. ८ ७ × १ २ १

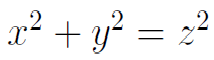
 } मी अमूर्त गणितात सध्या पीएचडी करत आहे. आज जरा गणिताविषयी लिहीन. पुढे कधीतरी मी स्वतः काय करतो याबद्दल माहिती देईन.
} मी अमूर्त गणितात सध्या पीएचडी करत आहे. आज जरा गणिताविषयी लिहीन. पुढे कधीतरी मी स्वतः काय करतो याबद्दल माहिती देईन.