पायथागोरसची त्रिकूटे

Submitted by भास्कराचार्य on 8 November, 2013 - 19:25

उपोद्घात

पायथागोरसच्या प्रमेयाबद्दल ऐकले नसेल, असे सहसा होत नाही. जवळपास प्रत्येकाने लहानपणी

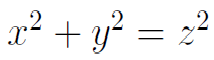
Pythagoras_equation.png

हे समीकरण पाहिलेले आहे. पायथागोरसची त्रिकूटे म्हणजे ह्या समीकरणाच्या अशा उकली, ज्यामध्ये प्रत्येक x, y, z पूर्णांक आहेत. उदा. (३, ४, ५) , (५, १२, १३) , (८, १५, १७) , (६, ८, १०) इ. ह्यांबद्दल सुद्धा आपण ऐकले असेल. अशी किती त्रिकूटे आहेत? सगळी सांगता येतील का? असा प्रश्न विचारता येऊ शकतो. आज आपण ह्याच प्रश्नाकडे बघू.

प्राथमिक माहिती

पायथागोरसचे प्रमेय खरे तर भूमितीतले विधान आहे. "कुठलाही काटकोन त्रिकोण दिला असता त्याच्या बाजूंची लांबी जर a, b, c (c हा कर्ण) असेल, तर a^2 + b^2 = c^2 हे खरे असते." आणि "उलटपक्षी, कुठल्याही ३ अशा संख्या दिल्या असता तेवढी लांबी असलेल्या बाजू घेऊन काटकोन त्रिकोण बनवता येतो." अशी दोन विधाने त्यात आहेत. परंतु, ह्यामध्ये कुठेही a, b, c तिन्ही पूर्णांक घेता येऊ शकतात अशी हमी दिलेली नाही. फक्त पायथागोरसच्या प्रमेयावरून 'तिन्ही बाजू पूर्णांक असलेले काटकोन त्रिकोण अस्तित्वात असतात का?' हे सांगता येत नाही. काही जणांचा गोंधळ यात होऊ शकतो, म्हणून मुद्दाम थोडासा इशारा.

'(a, b, c) पूर्णांक घेता येऊ शकतात का?' ह्यासारखे प्रश्न डायोफँटस ह्या ग्रीक गणितज्ञाने प्रथम विचारले असे म्हणायला हरकत नाही. त्याने हा प्रश्न पूर्णांक सहगुणक (Integer Coefficients) असलेल्या सर्वच समीकरणांसाठी मांडून तो सोडवायचा प्रयत्न केला. अशा समीकरणांना Diophantine Equations म्हटले जाते. उदा. 2x + 4y = 1, 3x^2 + 4y^2 = 5z^2, x^3 + y^3 = a^3 - b^3, Nx^2 + 1 = y^2, इ.

(येथे नमूद केले पाहिजे, की ब्रह्मगुप्त, आर्यभट, भास्कराचार्य, इ. यासारख्या भारतीय गणितज्ञांनी सुद्धा अशी काही समीकरणे पूर्णांकांमध्ये सोडवण्यात बरीच गरूडझेप घेतली होती. 'कुट्टक' व 'चक्रवाल' अशा पद्धती त्यांनी शोधून काढल्या होत्या. त्यांबद्दल पुढे कधीतरी.)

ही सर्वच समीकरणे सोडवायची एक सरसकट पद्धत अशी नाही. विशेषतः घात (power) वाढत जाईल तसे हे काम अवघड होत जाते. वरील 2x + 4y = 1, 3x^2 + 4y^2 = 5z^2 ह्या दोन्ही समीकरणांना पूर्णांकांत उकल नाही हे सांगता येते. पैकी पहिले उदाहरण अगदी सोपे आहे, दुसरे बरेच अवघड. पहिल्याचा विचार करून पाहा. (कोणी विचारल्यास मी सांगेनच.)

आपण ह्यातले फक्त x^2 + y^2 = z^2 हे पायथागोरस समीकरण आता पाहूया.

मूळ उकली (Primitive Solutions)

थोडासा विचार केल्यास लक्षात येईल, की (x, 0, x) हे कुठल्याही पूर्णांक x साठी पायथागोरसचे त्रिकूट आहे. परंतु हे म्हणजे थोडीशी पळवाट झाली. आपल्या उकलीत 0 असेल, तर तिला Trivial म्हणू. अशा Trivial गोष्टी आपल्याला नको. यापुढे फक्त non-trivial त्रिकूटे आहेत का, ह्याचाच विचार करूया.

ह्यानंतरही, प्रयत्नप्रमादपद्धतीने (Trial and Error) पायथागोरस समीकरणाची उकल सहज होते. वर म्हटल्याप्रमाणे (३, ४, ५) हे पूर्णांक ह्या समीकरणाचे समाधान करतात. त्यामुळे 'आहेत की नाहीत' ला उत्तर 'आहेत' असे सहज देता येते. ('नाहीत' असे उत्तर द्यायला जास्त कष्ट लागले असते कदाचित.)

परंतु एवढ्यावरच समाधान झाले तर अजून काय पाहिजे! ह्याच्या उकली अनंत (infinite) आहेत की सांत (finite) हे कळू शकेल का? असा प्रश्न विचारला गेला. (म्हणजेच, असे अनंत त्रिकोण शोधले जाऊ शकतात का? असा प्रश्न.) थोडा विचार केल्यावर लक्षात येते, की त्रिकोणांच्या सरूपतेने (similarity) हे सुद्धा अगदी सहज सांगता येऊ शकते. (३, ४, ५) मध्ये प्रत्येक संख्येला २ ने गुणल्यावर (६, ८, १०) हे त्रि़कूट मिळते. हा त्रिकोण आधीच्या त्रिकोणाशी सरूप आणि म्हणूनच काटकोन असणार हे उघड आहे. म्हणूनच (६, ८, १०) ही सुद्धा पायथागोरस त्रिकोणाची उकल आहे. त्याच प्रकारे ३ ने गुणून (९, १२, १५), ४ ने गुणून (१२, १६, २०) इत्यादी त्रिकूटे मिळतात. नैसर्गिक संख्या अनंत असल्याने प्रत्येकीने गुणून अशी अनंत त्रिकूटे मिळवता येऊ शकतात असे दिसते.

पण हीसुद्धा वर म्हटल्याप्रमाणे पळवाट झाली. थोडी जास्त हुषारीची, पण पळवाटच. त्यामुळे हीसुद्धा आपण बंद करून टाकूया. वरील नवीन तयार झालेल्या त्रिकूटांमध्ये तिन्ही संख्यांना १ पेक्षा मोठा सामाईक विभाजक आहे, असे दिसते. (कारण ती एकाच संख्येने गुणून बनलेली आहेत.) अशी त्रिकूटे आपण त्यांच्या पहिल्या त्रिकूटांबरोबर मोजली असे म्हणायला हरकत नाही. अशा तर्‍हेने आपण पुढील व्याख्या पाळणारी त्रिकूटेच मोजायचा प्रयत्न करूया.

व्याख्या : (a, b, c) हे जर पायथागोरसचे त्रिकूट असेल, आणि a, b, c ह्यांचा मसावि १ असेल, (जेणेकरून १ पेक्षा मोठा सामाईक विभाजक नाही) तर त्याला 'मूळ त्रिकूट' असे म्हटले जाईल. {a, b, c पैकी कुठलीही 0 नसल्याने ही व्याख्या करण्यात अडचण येत नाही.}

तर, आता आपला प्रश्न "पायथागोरसची मूळ त्रिकूटे अनंत आहेत का?" असा आहे. त्यात मी अजून थोडी भर घालतो आणि आपला प्रश्न "ती सांत असली, तर सगळी लिहा. अनंत असली तर त्यांना एखादा common form आहे का? ते सांगा." असा करतो. म्हणजेच "एखादा फॉर्म्युला आहे का, ज्याने ती सर्व निर्माण करता येतील?" (सांत किंवा अनंत)

टीपः अशा फॉर्म्युल्याची अपेक्षा करणे अवाजवी वाटेल, परंतु बर्‍याच वेळा तसा तो असतो. किंबहुना, इथूनच त्याची सुरवात झाली असे म्हणता येईल.

वक्रांवरील बिंदू (Points on Curves)

ही आजची Technique आहे. मी वरील समीकरणाच्या उकलींची आता एका वेगळ्याच भौमितीक प्रश्नाशी सांगड घालतो.

Circle_equation.png

हे XY-प्रतलातील वर्तुळाचे समीकरण आहे हे बहुतेकांना माहीत असेल. {केंद्रबिंदू (0, 0)}

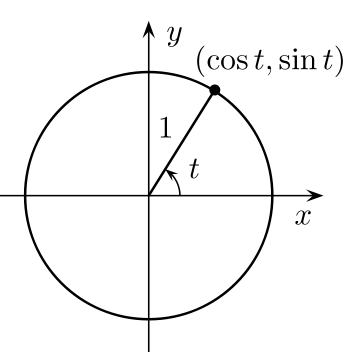
352px-Unit_circle.svg_.png

ह्या समीकरणाचा आणि आपल्या पायथागोरस समीकरणाचा संबंध लावता येतो. पायथागोरस समीकरणात z^2 ने दोन्ही बाजूंस छेद दिल्यास (आपण z हा 0 नाही अश्या उकली बघणार असल्याने ह्याने फरक पडणार नाही.) आपल्याला (x/z)^2 + (y/z)^2 = 1 असे येते.

म्हणजेच, (a, b, c) ही पायथागोरस समीकरणाची उकल जर असेल, तर त्याचा संबंध (correspondence) वर्तुळावरच्या (a/c , b/c) ह्या बिंदूशी लावता येतो. उलटपक्षी, जर (p/r , q/r) हा जर वर्तुळावरील बिंदू असेल, तर त्याचा संबंध छेद नाहीसे केल्यानंतर तयार होणार्‍या (p, q, r) ह्या उकलीशी लावता येतो.

जर (a, b, c) हे तिन्ही पूर्णांक असतील तर? तर वर्तुळावरच्या संबंधित बिंदूचे को-ऑर्डिनेट्स हे परिमेय (rational) असतात. अशा बिंदूंना 'परिमेय बिंदू' (rational points) म्हणू. त्याच प्रकारे, वर्तुळावरचा असा बिंदू मिळाल्यास संबंधित त्रिकूटातील तिन्ही संख्या पूर्णांक असतील. तसेच, आपल्याला लक्षात येईल, की एकाच मूळ त्रिकूटाला गुणून जी त्रिकूटे येतात, ती (आणि ते मूळ त्रिकूट) सर्व वर्तुळावरील एकाच बिंदूशी संबंधित असतात. ह्याचाच अर्थ, जर वर्तुळावरील सर्व परिमेय बिंदू सांगण्याचा एखादा मार्ग जर मिळाला, तर सर्व मूळ त्रिकूटे सांगता येतील.

हीच पद्धत गणितात फार महत्वाची आहे. (Counting Rational Points on Curves) ह्याचा एक वेगळाच उपयोग नंतर निदर्शनास आला. त्याविषयी थोडक्यात लेखाच्या शेवटी लिहितो.

[येथून पुढचा भाग थोडा जास्त तांत्रिक आहे, त्याबद्दल क्षमस्व. परंतु ज्यांना १२वीपर्यंत गणित होते, अशांना थोडा प्रयत्न करून वाचता यायला हरकत नाही असे मला वाटते. न कळल्यास सरळ शेवटचा फॉर्म्युला बघितल्यास हरकत नाही.)

वर्तुळावरील परिमेय बिंदू (Rational Points on the Circle)

आपण आपला प्रश्न रूपांतरित केला खरा, पण त्याचा काही फायदा आहे काय? असा विचार मनात येऊ शकतो. एका कठीण प्रश्नाचा आपण दुसरा तेवढाच कठीण प्रश्न बनवला नाही ह्याची काय खात्री? परंतु ह्या बाबतीत आता आपण भूमितीच्या कल्पना वापरून अतिशय सुंदररीत्या उत्तराप्रती पोहोचू शकतो. (मागे एका लेखात मी म्हटले होते, की एकीकडची tools वापरून दुसरीकडचे न सुटणारे प्रश्न सोडवता येऊ शकतात.) ते पुढीलप्रमाणे -

(1, 0) हा बिंदू वर्तुळावर आहे हे अगदी सहज दिसते. हा बिंदू आपल्याला नको, कारण तो trivial त्रिकूटाशी संबंधित आहे. परंतु ह्याचा वापर करून आपण नवीन बिंदू तयार करूया.

(1, 0) मधून जाणारी, slope = -t असलेली सरळ रेषा (-t निवडायचे कारण काही खास नाही. फॉर्म्युला चांगला दिसावा म्हणून उगाच.)

Equation_of_line.png

ही आहे. ही रेषा वर्तुळाला दोन बिंदूंमध्ये छेदते. पैकी एक (1, 0) हा आहे. दुसरा बिंदू आपल्याला या रेषेचे समीकरण वर्तुळात substitute करून मिळेल.

Circle_equation.png मध्ये Equation_of_line.png घातले, की येते -

Line_in_circle.png

हे समीकरण Quadratic Equation आहे. हे अगदी सहज सोडवता येते. त्यातून आपल्याला दुसर्‍या बिंदूचा X co-ordinate मिळतो. तो आहे -

x_co-ordinate.png

तो रेषेच्या समीकरणात वापरून आपल्याला Y co-ordinate सुद्धा मिळतो. तो असा -

y_co-ordinate.png

ह्यावरून आपल्याला त्रिकूटासाठी पुढील फॉर्म्युला मिळतो -

solution.png

उलटपक्षी, जर का कुठला परिमेय बिंदू वर्तुळावर असेल, तर त्याला आणि (1 , 0) ला जोडणार्‍या रेषेचा slope, हा slope च्या व्याख्येमुळे, परिमेय (m/n) असतो आणि मग त्या बिंदूचे co-ordinates वरील फॉर्म्युल्यातच बसतात.

आणि म्हणूनच, वरील फॉर्म्युला पायथागोरसची सर्व मूळ त्रिकूटे (खरे तर सगळीच त्रिकूटे) देतो असे आपण दाखवून दिलेले आहे.

उपयोग

पायथागोरसच्या प्रश्नामुळे आपली 'परिमेय बिंदू मोजणे' ह्या पद्धतीशी ओळख झाली. वर्तुळासारख्या 'चांगल्या' वक्राच्या (curve) बाबतीत एका परिमेय बिंदूपासून इतर सर्व बिंदू मिळवता येतात. (कारण रेषा ज्या दुसर्‍या बिंदूमध्ये छेदते, तोसुद्धा परिमेय निघतो.) परंतु इतर बाबतीत हे काम इतके सोपे नाही. सर्वसाधारणपणे वक्रावरील बिंदू शोधणे अवघड असते. दोन बिंदू दिले असता त्यांचे एकमेकांशी नाते शोधणेही अवघड असते. ह्या अवघडपणाचा वापर Computer Security मध्ये केला जातो. (Elliptic Curve Cryptography सर्च करून पहा.) त्याबद्दल पुन्हा कधीतरी लेख लिहिण्याचा प्रयत्न करेन. पूर्णांकांशी संबंधित एका साध्याशा प्रश्नातून अशी छान पद्धत निर्माण झाली हेच आश्चर्यकारक आहे.

(वरील चित्र विकीपीडिया वरून साभार.)

विषय: 
अवांतर
शब्दखुणा: 
गणित
पायथागोरस
नंबर थिअरी
त्रिकूटे
Groups audience: 
विज्ञान
Group content visibility: 
Public - accessible to all site users
शेअर करा

बापरे, बरंच लिहिलंय. मी एकदा वाचलं पण पुन्हा सावकाशीने वाचणार. गणित आमचा शत्रू नंबर १ राहिला आहे कायम. Happy

Submitted by नंदिनी on 8 November, 2013 - 22:43

पायथ्यागोरसची त्रिकुटे अनंत आहेत. काटकोन त्रिकोणाच्या भुजांचे काँबो अनंत असतील , तर त्रिकुटेही अनंतच निघतील.

त्यात काही मजेशीर काँबोही आहेत.

एक विषम संख्या घ्या.

त्याचा वर्ग करा.

हा वर्गही विषमच असेल.

त्याचे एकच्या फरकाने दोन भाग करा.

मूळची विषम संख्या आणि या दोन संख्या हे त्रिकुट झाले.

उदा. ३ चा वर्ग ९, त्याचे दोन भाग ४,५
५ चा वर्ग २५, त्याचे दोन भाग १२, १३
९९ चा वर्ग करा, त्याचे दोन भाग करा.

आता एक वैदिक प्रश्न.

एका राजाला १०० यज्ञ करायचे होते. अट होती की पहिल्या यज्ञाच्या दुप्पट क्षेत्रफळ दुसर्‍या यज्ञाचे हवे. अश प्रकारे १०० यज्ञांसाठी खड्डे खणायचे होते. तर यासाठी यज्ञाच्या बाजूसाठी काही फॉर्म्युला मिळेल का? Happy सर्व यज्ञ चौरस आकारात आहेत.

Submitted by संजिव पिल्ले on 8 November, 2013 - 23:14

तर यासाठी यज्ञाच्या बाजूसाठी काही फॉर्म्युला मिळेल का?>>>
प्रत्येक चौरसाची बाजू = (पहिल्या चौरसाचं क्षे.फ. X (२चा चौरसाचा नं.-१ घात)) यासगळ्याचं वर्गमूळ
हे वैदिक नाही पण यानी जमू शकेल . वैदिक कसे ते सांगा.

Submitted by जो_एस on 9 November, 2013 - 00:04

२ च्या वर्गमुळाने गुणायचे.

चौरसाच्या कर्णाइतकी बाजू घेऊन काढलेला दुसरा चौरस दुप्पट क्षेत्रफळाचा असतो.

त्यामुळे एक चौरस खड्डा खणायचा. मग दोरी घेऊन त्याचा कर्ण मोजायचा. तेवढी बाजू घेऊन दुसरा चौरस खड्डा खणायचा.

Submitted by संजिव पिल्ले on 9 November, 2013 - 00:18

वरती विषम संख्या घेऊन त्रिकुट मिळवायची पद्धत दिली आहे.

कोणतीही सम संख्या घेऊनही असेच त्रिकूट तयार करता येईल का? ( येते! Happy सूत्र काय असेल? )

Submitted by संजिव पिल्ले on 9 November, 2013 - 00:21

भारी आहे हे. गणित माझा १ नंबरचा मित्र, पण १२वी नंतर दुरावलेला. असा कुठे अवचित भेटला की लईच आनंद होतो.

संजिव पिल्ले,

side of n^th yadnyakunda = {square root of (n)} into X

where, X = side for first yadnyakunda where n = 1
for 2nd yandyakunda, n = 2
for 3rd yandyakunda, n = 3 and so on

Submitted by अश्विनी के on 9 November, 2013 - 00:40

संजीव पिल्ले, कुठल्याही सम (= 2m) संख्येसाठी

(2m)^2 + (m^2 - 1)^2 = (m^2 + 1)^2

वरच्या फॉर्म्युल्यात m = m आणि n = 1 घातल्यास हे सूत्र मिळते.

Submitted by भास्कराचार्य on 9 November, 2013 - 10:30

हो, बरोबर. जर t ची किंमत irrational असेल, तर वर्तुळावरचा irrational point मिळेल. आपल्याला फक्त रॅशनल हवे आहेत, म्हणून m/n असा घेतला.

Submitted by भास्कराचार्य on 9 November, 2013 - 11:13

भास्कराचार्य
लेख आवडला. इंग्रजी शब्दांचे मराठीतील प्रतिशब्द तुम्ही खूप सुरेख वापरता.

माझ्या पुढील शंका आहेत. .
t = m/n परिमेयच असेल असं का?
वरील सिध्दता 3D co-ordinates वापरून sphere/cone साठी अमलात आणता येते का?

Submitted by श्रीयू on 9 November, 2013 - 13:21

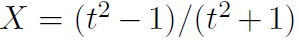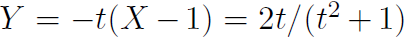t परिमेयच असेल असे नाही. आपल्याला x_co-ordinate.png आणि y_co-ordinate.png हे दोन्ही परिमेय हवेत, त्यासाठी t ची परिमेय किंमतच घ्यायला हवी. इतर किंमतींनी जे बिंदू मिळतील, ते परिमेय नसतील आणि आपल्याला ते नकोच आहेत.

वरील सिद्धता 3-d co-ordinates मध्ये sphere साठी अमलात आणता येते. फार छान प्रश्न विचारलात तुम्ही. बिंदूंसाठी आपल्याला पुढील फॉर्म्युला मिळतो -

x = 2s / (1 + s^2 + t^2)

y = 2t / (1 + s^2 + t^2)

z = (1 - s^2 - t^2) / (1 + s^2 + t^2)

जर आपण s, t परिमेय घेतले, तर आपल्याला x, y, z च्या परिमेय किमती मिळतील. (वरील फॉर्म्युला पाहून n-dimensional sphere साठी देखील ही सिद्धता देता येईल असे वाटते. फॉर्म्युल्यामधील रचनाक्रम उघड आहे.)

Submitted by भास्कराचार्य on 9 November, 2013 - 19:45

<उलटपक्षी, जर का कुठला परिमेय बिंदू वर्तुळावर असेल, तर त्याला आणि (1 , 0) ला जोडणार्‍या रेषेचा slope, हा slope च्या व्याख्येमुळे, परिमेय (m/n) असतो आणि मग त्या बिंदूचे co-ordinates वरील फॉर्म्युल्यातच बसतात.>
sorry missed this point.

Submitted by श्रीयू on 9 November, 2013 - 19:48

संजिव पिल्ले,

>> एका राजाला १०० यज्ञ करायचे होते. अट होती की पहिल्या यज्ञाच्या दुप्पट क्षेत्रफळ दुसर्‍या यज्ञाचे हवे. अश
>> प्रकारे १०० यज्ञांसाठी खड्डे खणायचे होते. तर यासाठी यज्ञाच्या बाजूसाठी काही फॉर्म्युला मिळेल का?
>> सर्व यज्ञ चौरस आकारात आहेत.

तुमच्या राजाला याड लागलं का खूळ! Wink

सुरुवातीच्या चौरसाचं क्षेत्रफळ a धरलं तर n+1 व्या चौरसाचं क्षेत्रफळ A असं येईल :

A = a * 2^n

आपण भातुकलीच्या यज्ञकुंडापासून सुरुवात करूया. वीतभर (२५ सेमी) लांबीरुंदीचं आहे हे कुंडं.

म्हणून, a = 25 * 25 sq cm = 625 sq cm = सव्वासहाशे चौरससेमी = सव्वासहाशे चौसेमी

आता चौरस सेमीचे चौरस मीटर करूया.

10000 चौसेमी = १ चौमी

म्हणून a = 0.0625 sq m = (1/16) sq m

आता A = पृथ्वीचं क्षेत्रफळ धरूया. पृथ्वी हा घन्गोल असून त्याची त्रिज्या 6400 किमी आहे.

A = 4 * pi * 6400 * 6400 sq km, where pi = 3.141592
A = 514718540.36415172418971949191643 sq km

चौरस किमी चे चौरस मीटर्स करायचे झाले तर दहा लाखाने गुणावे लागते. यासाठी दशांश स्थळ ६ घरे उजवीकडे सरकवावे लागेल.

म्हणून A = 514718540364151.72418971949191643 sq m

तर A/a हे गुणोत्तर येते 8235496645826427.5870355118706629

म्हणून 2^n = A/a = 8235496645826427.5870355118706629

म्हणून
n = log 8235496645826427.5870355118706629 / log 2 = 52.87077707
= 52 (nearest integer)

याचा अर्थ असा की ५३ (=५२+१) चौरस काढून झाले की ५४ व्या चौरसाला पृथ्वी अपुरी पडेल. शिवाय १ ते ५३ चौरस खड्डे आहेतंच!

हा कुठला यज्ञ आहे बरे! आणि कोण अरण्यपंडित पौरोहित्य करतोय! Lol

आता विषय निघालाच आहे तर आकडेमोड पुढे चालू ठेवूया. जर सूर्य ते पृथ्वी हे अंतर एक भुजा धरली तर किती क्षेत्र उपयोगास येईल ते बघूया.

सूर्य पृथ्वीपासून सुमारे १५ कोटी किमी अंतरावर आहे.

A = 15 koti * 15 koti sq km
= 225 e 14 sq km
= 225 e 20 sq m

a = 0.0625 sq m = (1/16) sq m

A/a = 16 * 225 e20 = 3600e20

म्हणून 2^n = 3600e20
म्हणून n = log (3600e20) / log 2 = 78.25 = 78 (nearest integer)

याचा अर्थ ७९ वा चौरस धडपणे मावेल. ८० व्या चौरसास जागा अपुरी पडेल.

तर १०० व्या चौरसाची भुजा किती येईल ते बघूया.

A = a * 2^n

n = 99, a = 0.0625 sq m

म्हणून A = 39614081257132168796771975168 sq m

म्हणून अशा चौरसाची एक भुजा
= sqrt (A) = 199032864766430.3926444941987038 m
= 2e14 m

प्रकाश एका सेकंदात ३ लाख किमी (3e8 m) जातो. ही भुजा पार करायला प्रकाशाला किती वेळ लागेल ते पाहू :
2e14/3e8 secs
= (2/3)e6 secs
= (2/3/3600)e6 hrs
=(2/3/3600/24)e6 days
= (7.7160e-6)e6 days
= 7.71 days = 7 days 17 hrs 11 mins 6.666667 secs
= सुमारे पावणे आठ दिवस.

म्हणून शंभराव्या कुंडाची भुजा पावणे आठ प्रकाशदिवस आहे. सहज म्हणून प्रकाशाच्या वेगाने निघालो तरी पूर्ण कुंडास प्रदक्षिणा घालायला एक महिना (३१ दिवस) आरामात लागेल!

आता खड्डा कुठे खणायचा ते ठरवा बुवा! Proud

ही अवाढव्य अंतरे आपल्या आकाशगंगेच्या मानाने नगण्य आहेत. आपल्याला सर्वात जवळचा तारा अल्फा सेटॉरी हा साडेचार प्रकाशवर्षे दूर आहे. त्यासमोर पावणेआठ प्रकाशदिवस म्हणजे किस झाड की पत्ती!

आ.न.,
-गा.पै.

टीप :
१. इंग्रजी आकड्यांबद्दल क्षमस्व!
२. उदय यांचे चूक दाखवून दिल्याबद्दल आभार! Happy चुकीची दुरुस्ती केली आहे.

Submitted by गामा_पैलवान on 13 November, 2013 - 09:57

तुमच्या राजाला याड लागलं का खूळ! डोळा मारा
सुरुवातीच्या चौरसाचं क्षेत्रफळ a धरलं तर n-1 व्या चौरसाचं क्षेत्रफळ A असं येईल :
A = a * 2^n
------- गामा साहेब... n-१ व्या चौरसाचं क्षेत्रफळ a * २^n-२ असे असायला हवे, कृपया तपासुन बघाल का?

आता पहिला यज्ञ ०.००० ००० ००० ००१ मिटर x ०.००० ००० ००० ००१ मिटर म्हणजे १ x १०^-२४ चौरस मिटर अशा माफक क्षेत्रफळात केल्यास १०० व्या यज्ञासाठी आपल्याला केवळ ७९६ मिटर x ७९६ मिटर = ६३४००० चौरस मिटर असे क्षेत्रफळ लागेल.

आपण त्या काळात खुप खुप प्रगत होतो असे म्हटले जाते Wink (पुष्पक विमाने उडवत होतो, टेस्ट ट्युब बेबी तयार करत होतो तसेच विविध प्रकारची क्षेपणास्त्र उडवत होतो....) तर तर यज्ञासाठी ०.००० ००० ००० ००१ मिटर काही अशक्य कोटीतली गोष्ट नसावी. त्यामुळे हे सर्व करणे सहज शक्य असावे.

Submitted by उदय on 10 November, 2013 - 20:44

कोणतीही सम संख्या घ्या.

तिचा वर्ग करा.

त्याला दोनने भागा.

मग जे येईल त्याचे दोनच्या फरकाने दोन भाग करा.

त्रिकूट मिळेल.

उदा. ४ चा वर्ग १६.

१६ भागिले दोन ८.
८ चे भाग ३ व ५

३ , ४, ५ हे त्रिकूट.

Submitted by संजिव पिल्ले on 10 November, 2013 - 22:57

तुम्ही डाक्टर कशाला झालात? लै गणित येतं की राव तुमास्नी.

पाय मोडून घरात आडवा पडलो होतो. करमणूक व्हायला इंटरनेट शिवाय काही साधन नव्हतं.

आमचा मोडका पाय बघून आजुबाजुचं पब्लिक आनंदानं भक्तिरसात न्हात होतं. माझ्यापुढे द*चरित्र, गु*चरित्र, **बोध, ** रक्षा, ** ता : जशी आहे तशी ! , अमुक म्हाराज तमूक म्हाराज ..... पब्लिकनं लई पुस्तकं ठेवली होती.

म्या दोन चार पानं वाचली आणि सगळी पुस्तकं भिरकाटून टाकली.

मग सहज म्हणून नेटावर पायथ्यागोरसचे प्रमेय नेमके कसे सिद्ध केले गेले, हे गुगलले आणि आठ दिवस अगदी सुखात गेले. Happy पायथ्यागोरसचे प्रमेय सत्तर ऐंशी पद्धतीनी सिद्ध केलेलं आहे. त्यात १२ वर्शाच्या पोरापासून ८० वर्षाच्या माणसापर्यंत , गणितातील ओ की ठो कळत नसलेल्य माणसापासून गणितात पी एच डी केलेल्या व्यक्तीपर्यंत सर्वांचा समावेश आहे.

नंतरचा कन्वलसन्स पिरिअड गणित आणि ह्यारी पॉटरने भरुन काढला. Happy

पायथ्यागोरस प्रमेयाची सिद्धता या विषयावरही भास्कराचार्य महोदयानी लिहिलं तर छान होईल.

Submitted by संजिव पिल्ले on 11 November, 2013 - 03:17

उमेश Biggrin
वर जे राजाचे उदाहरण आहे, तसे अनेक उदाहरणे केवळ आकडेमोड आणि केवळ दुपटिने काय होवु शकते, यासाठी असावेत.
काही आठवलेली उदाहरणे.

एक बेडुक प्रत्येकवेळी आधी मारलेल्या उडिच्या अर्ध्या अंतराची उडी मारतो. जर त्याची पहिली उडी, डबक्याच्या त्रिज्येइतकी असेल, तर त्याला डबक्याबाहेर यायला किती उड्या लागतील?

डॉप्लरच्या नियमानुसार आपण प्रचंड वेगात गेलो, तर आपल्याला लाल दिवा हिरवा दिसतो, असे म्हणुन एका स्त्रीने लाल सिग्नल तोडल्याचा इन्कार केला. न्यायाधिशांनी ते स्वीकारुन, वेगमर्यादेचे उल्लंघन केले, म्हणुन प्रति १० किमी अधिक वेगाला १ रुपया दंड ठोठावला... तर ती स्त्री आनंदी होईल की दु:खी?

आणि असे बरेच.

Submitted by विजय देशमुख on 11 November, 2013 - 20:42

एक बेडुक प्रत्येकवेळी आधी मारलेल्या उडिच्या अर्ध्या अंतराची उडी मारतो. जर त्याची पहिली उडी, डबक्याच्या त्रिज्येइतकी असेल, तर त्याला डबक्याबाहेर यायला किती उड्या लागतील?

अहो एकच बास कि नाहीतरी बेडक डब्क्याच्या बाजूलाच बसलेली असतात. (डराव डराव)

एकदा डिस्कवरी चॅनेलवर एक मजेशीर कोड ऐकल

पृथ्वीच्या परिघाभोवती एक दोरी घट्ट बांधली ही दोरी मुळ स्थितीच्या (पृथ्वीच्या) १ मीटर सर्व बाजूनी उचलायची ठरविली तर किती दोरी वाढवावी लागेल .

साधारणतः कुठल्याही व्यक्तीच्या मनात खूप लांबीची दोरी जोडावी लागेल असेच येईल पण
मग उकल काढण्याचा प्रयत्न करु

पृथ्वीचा त्रिज्या R मानल्यास परिघ 2 x (22/7) x R होईल

म्हणजेच मूळ दोरीची लांबी = 2 x(22/7) x R

आता पृथ्वीपासून १ मी उंच दोरी घेतल्यास = R become R+1

नवीन परिघ= 2 x (22/7) x (R+1)
=
वाढलेली दोरी = 2 x Pi x (R+1) - 2x Pi x R
= 2 Pi R + 2 Pi - 2 Pi R
= 2 Pi
= 2x 3.142
= 6.30 m approximately

Happy

Submitted by टिंबक टू on 12 November, 2013 - 08:50

टिंबक टू, साधं सोपं कोडं आणि उकल छान आहे ..

मेंदूला खुराक म्हणून वरची इतर कोडी सोडवून बघायला हवीत ..

हे साईन , कॉस हे कन्सेप्ट्स (?) थ्री डायमेन्शन्स् मधेही तसेच असतात का , बाजू ऐवजी प्लेन्स् ना अ‍ॅप्लिकेबल?

Submitted by सशल on 12 November, 2013 - 10:23

@ टिंबक टू

सहीच आहे हे. थोडा विचार केला तर कुठलाही गोळा असेल आणि दोरी त्या त्या गोळ्यापासून १ मी. उचलायची असेल तर प्रत्येक वेळा त्या त्या गोळ्याचा परीघ + २* pi एव्हढीच लांबी लागेल. हो ना?

Submitted by श्रीयू on 12 November, 2013 - 13:51

सशल
<हे साईन , कॉस हे कन्सेप्ट्स (?) थ्री डायमेन्शन्स् मधेही तसेच असतात का , बाजू ऐवजी प्लेन्स् ना अ‍ॅप्लिकेब>
बहुतेक थोडा बदल होतो. spherical trignometry चे formulae वेगळे असतात असं आठवतय.
गणित्तज्ञ आणिक प्राकाश टाकतीलच.

Submitted by श्रीयू on 12 November, 2013 - 13:55

गा. पै.,

ते पुराणात वामनाने पण असेच काहीतरी गणिती कोड्याने बलिकडे जागा मागितली असेल. बळी गणितात कच्चा असावा नाहीतर यज्ञाच्या घाईगडबडीत गणित सोडवत बसला नसावा.. म्हणून बिचार्‍याचे सगळे राज्य (पृथ्वीसकट) वामनाने दानात घेऊन टाकले असेल.

वरचे ते पृथ्वीच्या परिघाचे गणित बघा. वाटते किती लांब दोर लागेल, पण प्रत्यक्षात फक्त २ pi. तसेच बिचार्‍या बळीला वाटले असेल की टीचभर जमिनच लागेल, पण प्रत्यक्षात पृथ्वीच्यापेक्षा जास्त जमिन लागणार त्या यज्ञकुंडांना.

Submitted by राहुल१२३ on 12 November, 2013 - 14:38

मस्त!

सांत की अनंत हे उत्तर मात्र दिलंच नाही (नंतर ते आलं आहे अर्थात)

म्/न पासून त्रिकुटं मिळवतांना abs वापरावं लागेल ना?
नाहीतर क्ष^२ == (-क्ष)^२ असल्यानी -७ , २४, २५ अशी त्रिकुटं पण मिळतील.

रच्याकने, क्षेत्रफळ हे क्ष^२ सारखं असल्यानी पायथ्यॅगोरीयन त्रिकोणावर चौरसांऐवजी समत्रिभूज त्रिकोण (वगैरे) काढले तरी मोठ्याच्या क्षेत्रफळ इतर दोघांच्या बेरजेइतजी होणार.

Submitted by aschig on 12 November, 2013 - 20:02

उदय,

>> गामा साहेब... n-१ व्या चौरसाचं क्षेत्रफळ a * २^n-२ असे असायला हवे, कृपया तपासुन बघाल का?

चूक दाखवून दिल्याबद्दल धन्यवाद! Happy दुरुस्ती केली आहे.

आ.न.,
-गा.पै.

Submitted by गामा_पैलवान on 13 November, 2013 - 09:59

Pages