(टीप - या लेखाचा सहलेखक मायबोली वरील खगोलशास्त्रज्ञ आशिष (आश्चिग) आहे. त्यामुळे काही प्रश्न असल्यास त्याला विचारा.  )
)
वेगवेगळ्या व्यवसायात वेगवेगळे धोके असतात. खगोलशास्त्राचा धोका उल्कापाताने मरण्याचा नसतो (उल्कापाताने कोणीही मेले असल्याची नोंद नाही), अघटीत गोष्टींच्या (म्हणजेच अ-घडु शकणाऱ्या गोष्टींच्या) इ-मेल उत्पाताचा असतो. 'पळा-पळा, सारे ग्रह रांगेत उभे आहेत', 'पहा-पहा, एका महीन्यात पाच-पाच शूक्रवार, शनिवार, सूर्यवार' वगैरे. त्यामुळे खऱ्याखुऱ्या (आणि) दुर्मीळ गोष्टींकडे मात्र सपशेल दुर्लक्ष होते. अशीच एक अति-दुर्मीळ आणि खगोलशास्त्राकरता ऐतिहासीक महत्व असलेली घटना येत्या ५-६ जूनला होऊ घातली आहे. तुमच्या-आमच्याच नाही, तर सध्या हयात असलेल्या सर्वांकरताच पृथ्वीवरून शुक्राची ही सुर्याबरोबर होणारी युती पहायचा शेवटचा योग आहे.
चंद्रांचे पृथ्वीभोवती फिरण्याचे आणि पृथ्वीचे सूर्याभोवती फिरण्याचे प्रतल एक नसल्याने दर महिन्याला चंद्र-सूर्य ग्रहणं होत नाहीत. त्याचप्रमाणे शुक्राची कक्षा पृथ्वीच्या कक्षेच्या पातळीशी करत असलेल्या ३.४ अंशांच्या कोनामुळे शुक्र, पृथ्वी आणि सूर्य जरी जवळ जवळ एका रांगेत दर ६०० दिवसांनी येत असले (तळटीप [१] पहा) तरी प्रत्यक्ष युती मात्र २४३ वर्षात ४ वेळाच होते, ते ही आठ वर्षांच्या फरकाने दोनदा! २००४, २०१२, आणि नंतर एकदम २११७ (आणि नंतर २१२५, २२४७ वगैरे). ही युती कुठून आणि केव्हा बघता येईल त्याचा हा सुंदर नकाशा . लेख वाचा अथवा वाचू नका, पण पहायला मात्र विसरु नका. खंडग्रास सूर्यग्रहणाच्या वेळी घ्याल तीच काळजी ही युती बघताना पण घ्या.
जरी ती इतकी दुर्मिळ घटना आहे तरी तिचा 'सूर्यापासून पृथ्वीचं अंतर कसं मोजलं?' या डोक्याला खिट्टी लावणार्या प्रश्नाचं उत्तर शोधण्याच्या प्रयत्नांशी निकट संबंध आहे. प्रकाशाला सूर्यापासून पृथ्वी पर्यंत यायला सुमारे ९ मिनिटं लागतात हे वाक्य आणि तत्सम अनेक वाक्यं शाळेत आपल्याकडून खूप वेळा घोटवून घेतलेली आहेत. पण एका आकड्या पलीकडे याची उपयुक्तता काय? ते कसं मोजलं? त्यामुळे अजून काय साध्य झालं? असे प्रश्न आपल्याला कधी पडले नाहीत किंवा पडले तरी त्यांना बगल दिली गेली. याचा इतिहास बघताना तेव्हाचं सर्वच विषयातलं तोकडं ज्ञान, ते ज्ञान वाढवण्याचा ध्यास घेतलेले शास्त्रज्ञ, त्यांचं चातुर्य व कल्पकता, त्यांचे कष्ट व धडपड, आलेल्या अनंत अडचणी, त्यातून मार्ग काढण्यासाठी दाखवलेली जिद्द तसंच त्या वेळची अपुरी, तुटपुंजी व बाल्यावस्थेतील साधन सामुग्री या असंख्य गोष्टी समोर येतात! या युतींचा मानवाचं खगोलशास्त्राचं ज्ञान वाढायला व एकंदरीत तंत्रज्ञानाच्या उन्नतीला खूपच फायदा झाला आहे
हे अंतर कशाला मोजायचं होतं? याचं कारण एकदा ते अंतर समजलं की केप्लरच्या<१> कृपेमुळं सूर्य आणि इतर सर्व ग्रहांमधली अंतरं एका झटक्यात मिळणार होती! त्याने, १६ व्या शतकात, त्याला उपलब्ध असलेल्या माहितीवरून एक फार महत्वाचा निष्कर्ष काढलेला होता (तळटीप [२] पहा). त्याला तो निष्कर्ष गणिताने सिद्ध करता आला नव्हता, तो नंतर न्यूटनने केला. तो म्हणजे ग्रहांचं सूर्यापासूनचं अंतर व त्यांना सूर्याभोवती फिरायला लागणारा वेळ (त्या ग्रहांचे 'वर्ष') यांचा एक साधा संबंध! तो वापरून सर्व ग्रहांचं अंतर AU (अॅस्ट्रॉनॉमिकल यूनिट) या एककात (युनिट) मांडता येतं. इथे १ AU म्हणजे पृथ्वी व सूर्य यामधील सरासरी अंतर. केप्लरच्या समीकरणाने ग्रहांची अंतरं अशी येतात - बुध ०.३८७ AU, शुक्र अंतर ०.७२३३ AU, पृथ्वी (अर्थातच) १AU, मंगळ १.५२ AU, गुरू ५.२० AU आणि शनी ९.५५ AU. थोडक्यात, एकदा का १ AU म्हणजे नक्की किती ते समजलं की सर्वच ग्रहांची अंतरं मिळणार होती. इतकंच नाही तर प्रत्येक ग्रहाचा व्यास पण समजणार होता. ग्रहांचा दुर्बिणीतला व्यास किती आहे हे माहिती होतं, त्यामुळे ग्रहांचं खरं अंतर समजल्यावर त्यांचा खराखुरा व्यास किती आहे त्याचा अंदाज येणार होता.
ग्रह तार्यांची अंतरं थोडी भूमिती वापरून काढता येतात. आकृती - १ मधे दिलेल्या काटकोन त्रिकोणाच्या पायाची लांबी (AC=b) व एक कोन (B=ABC) माहिती असेल तर उंची (BC=a), tan(B) = b / a या सूत्राने काढता येते.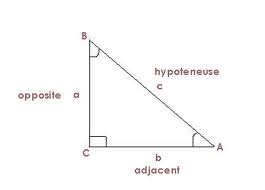
आकृती - १ : काटकोन त्रिकोण
ग्रह तार्यांची अंतरं काढण्याच्या वेळेला कोन B मोजण्यासाठी पॅरॅलॅक्स पद्धत वापरतात. पॅरॅलॅक्स म्हणजे दोन वेगळ्या ठिकाणांवरून एकाच वस्तूकडे पाहिल्यावर त्या वस्तूच्या जागेमधे दिसणारा बदल. उदा. एक पेन्सील हातात लांब धरून भिंतीवरच्या एखाद्या चित्राकडे पहा. नंतर एकदा डावा डोळा बंद करून व मग उजवा डोळा बंद करून पाहीलं तर ती पेन्सील चित्राच्या पार्श्वभूमिवर उजवी डावीकडे हललेली दिसेल. भूमितीच्या भाषेत बोलायचं झालं तर पॅरॅलॅक्स म्हणजे दोन वेगळ्या ठिकाणांवरून एकाच वस्तूकडे काढलेल्या दोन सरळ रेषां मधला कोन!
पॅरॅलॅक्स
---------
तारे प्रचंड अंतरांवर असल्यामुळे पॅरॅलॅक्स मिळविण्यासाठी प्रचंड लांबीचा पाया लागतो. अगदी पृथ्वीवरच्या दोन्ही धृवांपासून मोजमाप केलं तरी भागत नाही. त्यासाठी पृथ्वीच्या कक्षेचा वापर चतुरपणे करतात. तार्याची एका दिवशीची स्थिती आणि बरोबर ६ महिन्यानंतरची स्थिती घेतली तरच थोडासा पॅरॅलॅक्स दिसू शकतो. कारण पृथ्वी ६ महिन्यांनी बरोबर दोन विरुद्ध ठिकाणी असते व १ AU इतक्या प्रचंड लांबीचा पाया मिळतो. आकृती - २ व या साईट वरचे पॅरॅलॅक्स दाखवणारे अॅनिमेशनने पहा. अर्थात फार लांबवरच्या तार्यांसाठी हाही पुरेसा पडत नाही. जरी सर्व तारे गतिमान आहेत तरी त्यांच्या अति प्रचंड अंतरांमुळे आपल्याला ते वर्षानुवर्ष एकाच जागी दिसतात ते याच कारणामुळे (तळटीप [३] पहा)!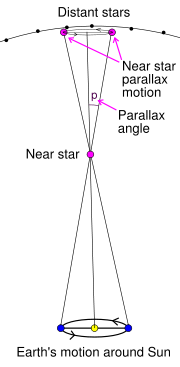
आकृती - २ : तार्याचा पॅरॅलॅक्स.
शुक्राने होणार्या सूर्य युतीचा सूर्य व पृथ्वी यातील अंतराशी कसा काय संबंध हा प्रश्न येणं साहजिकच आहे. त्याचं उत्तर फार पूर्वी इंग्रज खगोल शास्त्रज्ञ एडमंड हॅली<२> याने दिलं. या युतीचा वापर करून शुक्राचा सूर्याच्या पार्श्वभूमीवरील पॅरॅलॅक्स मोजणं शक्य आहे आणि अर्थातच त्यामुळे शुक्राचं पृथ्वीपासूनचं अंतर व पर्यायाने सूर्याचं पृथ्वीपासूनचं अंतर मिळवता येईल असं त्याचं म्हणणं होतं. शुक्र जेव्हा पृथ्वी आणि सूर्याच्या मधे येतो तेव्हा तो आपल्या सर्वात जवळ असतो. त्यामुळे त्याचा पॅरॅलॅक्स मोजण्यातील चूक कमित कमी होईल हा त्याचा होरा होता. आकृती ३ व ४ मधे या युतीचा पॅरॅलॅक्स पृथ्वी वरील दोन भिन्न ठिकाणावरून कसा दिसेल ते दाखवले आहे.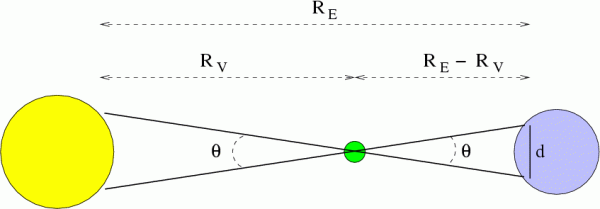
आकृती - ३ : पृथ्वीच्या दोन भिन्न ठिकाणांवरून शुक्राकडे मागे सूर्य असताना पाहिल्यास आकृती - ४ प्रमाणे शुक्र दोन भिन्न मार्गांनी सूर्याच्या चकतीवरून जाताना दिसेल.
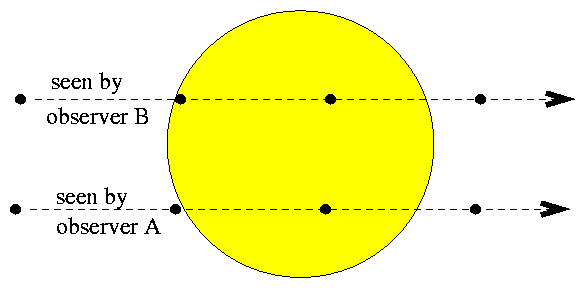
आकृती - ४ : शुक्र दोन भिन्न मार्गांनी सूर्याच्या चकतीवरून जाताना.
ही युती वेगवेगळ्या अक्षांशावरून पाहिल्यास शुक्राचा सूर्याच्या समोरून जायचा वेळ वेगवेगळा भरेल हे आकृती - ४ वरून स्पष्ट होतं. हॅलीच्या गणिताप्रमाणे, वेगवेगळ्या अक्षांशावरून मोजलेला युतीचा वेळ तसंच पृथ्वीचं स्वतःभोवतीचं भ्रमण इ. गोष्टी विचारात घेऊन, सूर्याचं अंतर काढणं शक्य होतं. पण सर्व स्थळांवरून एकाच वेळी मोजणं गरजेचं होतं. सूर्याच्या पुढे शुक्र नक्की कुठे कुठे असताना वेळा मोजायच्या त्या बाबतीत गोंधळ होऊ नये म्हणून आकृती - ५ मधे दाखवलेले ४ स्पर्श झाल्यावर मापन करायचं ठरवलं. ते असे - १> शुक्राची कड सूर्याला बाहेरून चिकटायची वेळ २> शुक्राची कड सूर्याच्या आतल्या बाजूकडून निसटायची वेळ ३> शुक्राची कड सूर्याच्या दुसर्या बाजूच्या आतल्या बाजूला चिकटायची वेळ ४> शुक्राची कड सूर्याच्या चकती पासून बाहेर पडायची वेळ. त्यातही सूर्याच्या प्रखर प्रकाशामुळे शुक्र जवळ येतानाचा, पहीला, किंवा बाहेर पडतानाचा, शेवटचा, नेमका क्षण मोजणं अवघड होतं! म्हणून भ्रमणाची वेळ ही तिसर्या व दुसर्या वेळांमधला फरक धरणार होते.
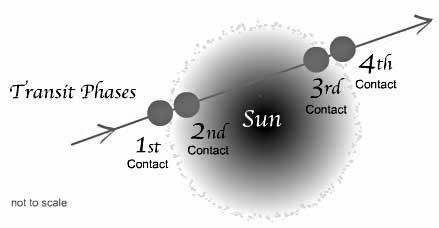
आकृती - ५ : शुक्राचे सूर्याशी होणारे ४ स्पर्शबिंदू!
हॅलीच्या नशिबात एकही युती नाही हे त्याला माहीत होतं. आधीची युती १६३१ व १६३९ साली होऊन गेली होती आणि पुढची ६ जून १७६१ व ३ जून १७६९ रोजी होणार होती. म्हणूनच त्यानं सर्व खगोल शास्त्रज्ञांना भविष्यातल्या युतींच्या वेळेला एकत्रित प्रयत्न करून पॅरॅलॅक्स मोजण्याचं आवाहन केलं होतं. १७४२ साली त्याचा देहांत झाला.
सूर्याच्या अंतरातली चूक कमी करण्यासाठी आणखी दोन गोष्टीतल्या चुका कमी करणं आवश्यक होतं. एक म्हणजे पायाची म्हणजे पृथ्वी वरील दोन भिन्न ठिकाणातली लांबी मोजणं आणि दुसरं म्हणजे पृथ्वीच्या भिन्न ठिकाणांवरील घड्याळं जुळवणं!
पायाची लांबी मोजण्यासाठी लागणारे अचूक नकाशे नशीबाने त्या काळापर्यंत तयार व्हायला लागले होते. एक काळ असा होता की स्थळाचा अक्षांश धृव तार्याचा क्षितिजाशी झालेला कोन मोजून अचूकपणे काढता यायचा. पण सगळा बल्ल्या रेखांश मोजताना व्हायचा! पृथ्वी स्वतः भोवती (म्हणजे ३६० डिग्री) २४ तासात फिरते, याचाच अर्थ ती दर तासाला १५ डिग्रींनी फिरते. त्यामुळे जर वेळ अचूक माहिती असेल तर आकाशातले तारे बघून रेखांश काढता येतात. त्यावेळी वापरात असलेली लंबकाची घड्याळं जहाजांवर बसणार्या हेलकाव्यांमुळे कुचकामी ठरायची. दिवसाकाठी पाच दहा मिनिटांनी घड्याळ हमखास चुकायचं, त्यामुळे दहा बारा दिवस समुद्रात काढले तर वेळेप्रमाणे येणारा रेखांश आणि प्रत्यक्षातला रेखांश यात चार पाचशे मैलांचा फरक सहज पडायचा. त्याचा परिणाम जहाजं भरकटणे किंवा खडकांवर आपटून जहाजं फुटून माल व मनुष्य हानी होणे यात व्हायचा. लांबवरच्या व्यापारासाठी प्रामुख्याने जहाजांचा वापर व्हायचा म्हणून अशी हानी कुठल्याही सरकारला परवडणारी नव्हती. त्यामुळेच अचूक रेखांश मोजू शकणार्या यंत्रासाठी मोठमोठी बक्षिसं जाहीर केली गेली. सगळ्यात मोठं वीस हजार पौंडाचं बक्षीस ब्रिटिश बोर्ड ऑफ लाँजिट्यूड या संस्थेनं जाहीर केलं.
जॉन हॅरिसन नावाच्या एका अशिक्षित सुताराने तसं घड्याळ बनवण्याचा ध्यास घेतला. आयुष्यातली जवळपास तीसेक वर्ष खर्ची घालून त्यानं विविध व वेगवेगळ्या अचूकतेची घड्याळं बनवली. त्याचं एक घड्याळ, १७६१ साली, एच. एम. एस. डेप्टफर्ड या जहाजावरून पोर्ट रॉयल जमैका येथे पोचेपर्यंत त्याच्यावरची वेळ फक्त ५.१ सेकंदांनी चुकली होती. पण त्यापुढे बरीच वर्षं लढूनही बिचार्याला बोर्डाकडून बक्षीसाचे पूर्ण पैसे काही मिळाले नाहीत!
गॅलिलिओने गुरूच्या चंद्रांनी होणार्या गुरुच्या युतींचा अभ्यास करून घड्याळांच्या वेळा जुळवण्याची एक पद्धत बनविली होती. प्रतिभेच्या या अप्रतिम आविष्काराबद्दल डच लोकांनी त्याला सोन्याची चेन बक्षीस म्हणून दिली. ही पद्धतही जहाजांवरून वापरण्यासारखी नव्हती कारण जहाजांच्या हेलकाव्यांमुळे कुठल्याही दुर्बिणीत ते चंद्र अवलोकन पूर्ण होईपर्यंत रहाणं शक्य नव्हतं. हीच पद्धत वापरून फ्रान्सचा अचूक नकाशा बनवला व पृथ्वीचा परीघ पण काढला. तो फक्त १२६ मैलांनी चुकला. फ्रान्सच्या नवीन नकाशावरून नंतर असं लक्षात आलं की फ्रान्स वाटलं होतं त्यापेक्षा आकाराने लहान आहे. त्यावर फ्रान्सच्या राजाने अशी टीका केली: फ्रान्सच्या सर्व शत्रूंनी आजपर्यंत जितका प्रदेश बळकावला नसेल त्यापेक्षा जास्त या नकाशा बनविणार्यांनी घालवला.
१६३१ सालची युती कुणीही पाहिल्याची नोंद नाही. १६३९ सालची युती दोघांनी बघितली होती पण तेव्हा फारशी उपयुक्त मोजमापं काही होऊ शकली नव्हती. शुक्राची चकती सूर्यापुढे 'आपल्या अपेक्षेपेक्षा फारच छोटी दिसली' या व्यतिरिक्त त्यात दुसरं लक्षवेधी काही नव्हतं.
पण ६ जून १७६१ च्या युतीच्या वेळी बर्याच सरकारांनी तो प्रतिष्ठेचा प्रश्न केला होता. बरेच पैसे या शास्त्रीय मोहिमेसाठी ओतले होते. सायबेरिया, दक्षिण आफ्रिका मेक्सिको अशा दूरदूरच्या एकूण ६२ ठिकाणी १२० शास्त्रज्ञ महागड्या उपकरणांसकट पाठवले होते. युतीच्या वेळी काही ठिकाणी निरभ्र आकाश मिळालं तर काही ठिकाणी ढगाळ! चार्लस मेसन व जेरेमाय डिक्सन यांना आफ्रिकेला पाठवलं होतं. वाटेत त्यांच्यावर फ्रान्सच्या बोटीने हल्ला केला (तेव्हा एक युद्ध पण चालू होतं). त्यात त्यांची ११ माणसं मेली व ३७ जखमी झाली. नंतर त्यांनी फ्रेंच सैनिकांच्या पहार्याखाली मोजमापं केली पण त्या दोघांच्या मोजमापात बर्याच सेकंदांचा फरक आला. विल्यम वेल्सनं कॅनडातल्या हडसन बे येथून डासांचा व कडाक्याच्या थंडीचा सामना करत मोजमाप केलं. थंडी इतकी कडक होती की त्यानं बाजूला ठेवलेल्या पाव लिटर ब्रँडीचा पाच मिनिटात बर्फ झाला.
ऑटेरोशे हा गोठलेल्या व्होल्गावरून रशियातल्या टोबोलस्क गावी युतीच्या ६ दिवस आधी पोचला. पण त्याने सूर्याच्या भ्रमणात हस्तक्षेप केल्यामुळे पूर आला म्हणून त्याच्यावर स्थानिक लोकांनी हल्ला केला. शेवटी त्याने रक्षकांच्या पहार्याखाली मोजमापं केली.
गिलोमे ले जेंटिल हा सगळ्यात जास्त दुर्दैवी म्हणावा लागेल. तो फ्रान्सहून २६ मार्च १७६० रोजी पाँडेचरीला निघाला. मान्सून मुळे त्याचं जहाज जे भरकटलं ते युतीच्या दिवशी देखील समुद्रातच होतं. त्यामुळे त्याला काहीही मोजमापं करणं शक्य नव्हतं. पण स्वतःची प्रतिष्टा जपण्यासाठी त्यानं तिथेच थांबून १७६९च्या युतीची मोजमापं करुनच परत जायचं ठरवलं. संपूर्ण मे महीनाभर निरभ्र असलेलं आकाश नेमकं युतीच्या दिवशी (जून ४) ढगाळलं ते युती संपल्यावर परत निरभ्र झालं. वैतागून त्यानं फ्रान्सला परत जायचं ठरवलं. पण वाईट पोट बिघडल्यामुळे त्याला पुढचे ९ महीने भारतातच रहावं लागलं. त्या नंतर तो एका स्पॅनिश जहाजावरून परत निघाला. ते जहाज केप ऑफ गुड होप पाशी वादळात सापडून भरकटलं. त्या नंतर तो कसाबसा फ्रान्स मधे सुमारे ११ वर्षांनी पोचल्यावर त्याला धक्काच बसला. तो मेला आहे असं जाहीर झालं होतं. त्याची बरीचशी मालमत्ता लुटलेली होती आणि उरलेली त्याच्या वारसांना वाटून टाकलेली होती.
१७६१ साली सर्वांच्या मापनात चुका झाल्या कारण आकृती ५ मधले दोन व तीन नंबरचे स्पर्श नक्की कधी झाले तेच ठरवणं अवघड झालं! कारण शुक्र सूर्याच्या जवळ असताना पाण्याच्या थेंबासारखा परिणाम दिसला. जेव्हा नळातून पाण्याचा एक थेंब हळूच पडतो तेव्हा तो नळापाशी, पाण्याच्या सर्फेस टेन्शन मुळे, ताणला गेल्यासारखा लांबट दिसतो. तसंच, दोन नंबरच्या बिंदूपाशी शुक्राची चकती सूर्याची कड सोडताना पाण्याच्या थेंबासारखी ताणली गेल्यासारखी दिसली. याच्या नेमकं उलट ३ नंबरच्या बिंदूपाशी झालं. शुक्राची चकती सूर्याला चिकटायच्या आधीच एक काळी रेषा शुक्रापासून निघून सूर्याला चिकटली व जसजसा शुक्र सूर्याच्या जवळ जायला लागला तसतशी ती रेषा ठळक व्हायला लागली. त्यामुळेच प्रत्येकाने मोजलेल्या स्पर्शांच्या वेळेत फरक आला.
अजून एक परिणाम म्हणजे सूर्या जवळ शुक्र एखाद्या प्रकाशमान कंकणात बद्ध दिसतो पण त्याची कड सावलीसारखी अस्पष्ट व फिकट दिसते. हा परिणाम शुक्रावरच्या वातावरणाचा असला पाहीजे असं अनुमान त्या वरून काढलं (जे नंतर बरोबर निघालं). तो पर्यंत कुणाला शुक्रावर वातावरण आहे याची कल्पना नव्हती. कारण वातावरणामुळे प्रकाशाचं वक्रीभवन होतं. सॅम्युएल डन या शास्त्रज्ञाने त्या सावलीला सूर्याची कड पार करायला लागलेल्या वेळावरून शुक्रावर सुमारे ५० मैलाचं वातावरण आहे असा निष्कर्ष काढला.
या सर्वांचा परिणाम सूर्याचं अंतर चुकण्यात झाला. ते साधारण ८१ ते ९८ दशलक्ष मैल या मधे असावं इतकाच तर्क बांधता आला. सध्याच्या मोजणी प्रमाणे खरं अंतर ९२, ९१०, ००० मैल आहे.
मागच्या युतीतून फारसं काही निष्पन्न न झाल्यामुळे ३ जून १७६९ रोजी होणार्या युतीसाठी जास्त प्रयत्न करायचं ठरवलं. एकूण ७७ ठिकाणांवर १५१ शास्त्रज्ञ पाठवले. या वेळेला युती बघताना काय समस्या येतात याचं ज्ञान होतं. म्हणून जास्त मोठ्या आणि चांगल्या दुर्बिणी दिल्या. त्यांना प्रतिमा कमी बिघडवणारी भिंगं लावलेली होती.
२६ ऑगस्ट १७६८ रोजी कॅप्टन कुकच्या नेतृत्वाखाली एच. एम. एस. एंडेव्हर प्लिमथ बंदरातून ताहितीकडे जायला निघाली. बोटीवर जोसेफ बँक्स हा शास्त्रज्ञ होता. शिवाय कुकही स्वतः चांगला गणितज्ञ होता. बोटीवर उपकरणांशिवाय एक पिंप भरून खिळे होते ते ताहितींशी व्यवहार करण्यासाठी घेतलेले होते. ताहिती लोकांना विशेषतः बायकांना धातुच्या कुठल्याही वस्तूंचं इतकं प्रचंड आकर्षण असतं की ते त्यांच्या बदल्यात कुठलाही सौदा करायला तयार असतात. कुकने सगळ्यांना परवानगीशिवाय कुणालाही ते खिळे द्यायचे नाहीत असा कडक दम भरला होता तरीही बोटीवरच्या धातुच्या वस्तू गायबच होत राहिल्या. या सर्व भानगडीतून त्यांनी ती युती व्यवस्थित पाहीली पण मोजमाप करताना घोटाळा झालाच. या वेळी चांगल्या दुर्बिणींमुळे थेंबासारखा परिणामही जास्त सुस्पष्ट व मोठा दिसला. म्हणून, कुक सकट सगळ्यांना शुक्र वेगवेगळ्या वेळांना सूर्याला चिकटला व बाहेर पडला असं वाटलं. त्यांच्या वेळांमधे वीस सेकंदांपर्यंत फरक होता. १७६९ च्या मापनातून सूर्याचं अंतर ९३ दशलक्ष मैलापासून ९७ दशलक्ष मैलापर्यंत भरलं. सध्याच्या अभ्यासानुसार तो थेंबासारखा परिणाम पृथ्वीचं वातावरण आणि दुर्बिणीतलं वक्रीभवन यामुळे दिसतो.
९ डिसेंबर १८७४ च्या युतीच्या वेळी सर्व निरीक्षकांना आधीच अपेक्षित मोजमाप पद्धतीचं प्रशिक्षण दिलं गेलं. त्यासाठी युतीचं सिम्युलेशन (नकली नाटकीकरण?) केलं गेलं. कुठल्या प्रकारच्या दुर्बिणी वापरायच्या ते ठरवलं. मुख्य म्हणजे कॅमेर्याचा शोध लागलेला असल्याने फोटो पण काढण्यात आले. या वेळेला जरी पाण्याच्या थेंबासदृश परिणामाचा त्रास कमी झाला तरी प्रकाशमान कंकणबद्ध शुक्र व त्याची अस्पष्ट व फिकट कड यामुळे फार काही चांगली मोजमापं झाली नाहीत. काढलेल्या फोटोंवरूनही काही वेगळा निष्कर्ष निघाला नाही म्हणून १८८२ च्या युतीच्या वेळी फ्रेंच शास्त्रज्ञांनी कॅमेरा न वापरण्याचा आग्रह धरला. १८८२ साली ९२, ८८०, ००० मैल इतकं अंतर काढलं गेलं जे सध्याच्या अंतरापेक्षा फक्त ३०, ००० मैलांनी कमी आहे.
रशियाने १९५७ साली स्पुटनिक अवकाशात उडवल्यावर अमेरिकेने पण अवकाश विज्ञान आपल्या प्रतिष्ठेचा प्रश्न केला. तो काळ त्या दोन राष्ट्रांमधल्या शीतयुद्धाचा होता. त्यामुळे अमेरिकेला रशिया उत्तर धृवावरून क्षेपणास्त्र फेकेल अशी भीती वाटत होती. क्षेपणास्त्र आल्याची सूचना देण्यासाठी उच्च शक्तीचा मायक्रोवेव्ह रडार एमआयटीतील तंत्रज्ञ, रॉबर्ट प्राइस व पॉल ग्रीन, बांधत होते. तेव्हा त्यांच्या डोक्यात असा विचार आला की त्यांच्या यंत्राने जवळच्या ग्रहाकडे लहरी पाठवल्या तर ग्रहाकडून परावर्तित झालेल्या क्षीण लहरी पकडण्याइतकं ते यंत्र चांगलं आहे का? त्याची परीक्षा घेण्यासाठी त्यांनी फेब्रुवारी १९५८ मधे पृथ्वी जवळ आलेल्या शुक्रावर लहरी सोडल्या. त्यातून समजलेलं शुक्राचं अंतर २८ दशलक्ष मैल (१ AU = ९३,४१६, ८७५ मैल) इतकं होतं. पण, दुर्दैवाने, सप्टेंबर १९५९ मधे शुक्र परत पृथ्वीच्या जवळ आल्यावर त्यांना त्या मापनाची पुनरावृत्ती नाही करता आली. अशातऱ्हेनं इप्सित साधण्यात जरी अपयश आलं तरी त्यातून अनेक नव्या गोष्टी पृथ्वीकरांना शिकायला मिळाल्या.
त्या नंतर रडार वापरून १ AU मोजण्यासाठी बरेच प्रयोग केले गेले आणि त्यातून जवळपासचे वेगवेगळे आकडे आले. शेवटी, १९६४ साली १ AU म्हणजे ९२, ९१०, ००० +/- १२५० मैल इतकं अंतर अशी घोषणा इंटरनॅशनल अॅस्ट्रॉनॉमिकल युनियनने केली.
या सगळ्याचा गोषवारा चर्चिलच्या शब्दात द्यायचा झाला तर तो असा देता येईल -- Success consists of going from failure to failure without loss of enthusiasm.
तळटीप [१] :- शुक्र, पृथ्वी व सूर्य एका रांगेत येण्याचा कालावधी
--------------------------------------------------------------------
शुक्राचे 'वर्ष' २२४ दिवसांचे, तर पृथ्वीचे ३६५ दिवसांचे. पृथ्वी/सूर्य/शुक्र एका रांगेत दोनदा येण्यामधील कालावधी हा ३६५*क्ष असा मांडता येईल. क्ष ची किम्मत अशी मिळेल: ३६५/२२४ = (क्ष + १)/क्ष = १.६
तळटीप [२] :- केप्लरचा तिसरा नियम
-----------------------------------------
कुठल्याही दोन ग्रहांना सूर्याभोवती फिरायला लागणार्या वेळांच्या गुणोत्तराचा वर्ग हा त्या ग्रहांच्या सूर्यापासूनच्या अंतराच्या गुणोत्तराच्या घनाच्या बरोबर असतो. केप्लरनं खालील समीकरण शोधलं -
(ग्रहाचा सूर्याभोवती फिरायचा वेळ / पृथ्वीचा सूर्याभोवती फिरायचा वेळ )^२ = (ग्रह व सूर्यातलं अंतर / पृथ्वी व सूर्यातलं अंतर )^३.
अर्थात, सर्व ग्रहांच्या कक्षा लंब वर्तुळाकार असल्यामुळे इथे सरासरी अंतर अपेक्षित आहे. कक्षा लंब वर्तुळाकार असल्या तरी त्या बर्याचशा गोलाकारच आहेत. सूर्यापासूनच्या सर्वात जवळच्या व सर्वात दूरच्या बिंदूंच्या अंतरात ४% पेक्षा कमी फरक आहे. यातल्या पृथ्वी व सूर्य यामधील सरासरी अंतराला १ अॅस्ट्रॉनॉमिकल यूनिट (AU) मानतात.
प्रत्येक ग्रहाला सूर्याभोवती फिरायला किती दिवस लागतात हे भरपूर निरीक्षणांमुळे माहीत झालेलं होतं. उदा. समजा, एखाद्या ग्रहाला सूर्याभोवती फिरायला ८ वर्ष लागतात. तर वरचं समीकरण असं लिहीता येईल.
( ८ )^२ = (ग्रह व सूर्यातलं अंतर / पृथ्वी व सूर्यातलं अंतर )^३.
६४ = (ग्रह व सूर्यातलं अंतर / पृथ्वी व सूर्यातलं अंतर )^३.
४ = (ग्रह व सूर्यातलं अंतर / पृथ्वी व सूर्यातलं अंतर )
म्हणजेच, (ग्रह व सूर्यातलं अंतर) = ४ AU.
तळटीप [३] :- अंतर व पॅरॅलॅक्स यांचं व्यस्त प्रमाण
-------------------------------------------------------
हा पॅरॅलॅक्स वस्तू जितकी जवळ तितका मोठा दिसतो. पण लांबच्या वस्तूंसाठी अगदी लहान असतो. उदा. आपल्या सगळ्यात जवळ असलेल्या, प्रॉक्सिमा सेंटॉरी (अंतर ४.२ प्रकाश वर्ष), तार्याचा पॅरॅलॅक्स फक्त ०.७६८७ आर्क सेकंद (१ डिग्री = ६० आर्क मिनीटं, व १ मिनीट = ६० आर्क सेकंद, म्हणून १ डिग्री = ३६०० आर्क सेकंद) इतकाच भरतो. जवळ जवळ इतकाच पॅरॅलॅक्स ५.३ किलो मीटर लांब ठेवलेल्या २ सेंटिमीटर व्यासाच्या वस्तू मुळे मिळेल. हा पॅरॅलॅक्स इतका बारीक असल्यामुळे तो मोजताना थोडी जरी चूक झाली तरी अंतरात बरीच मोठी चूक होते.
तळटीप [४] :- सूर्य ग्रहण
---------------------------
आपल्याला दिसणारा चंद्राचा आणि सूर्याचा आकार साधारणपणे सारखाच असल्यामुळे चंद्र जेव्हा सूर्य व पृथ्वीच्या मधे येतो तेव्हा तो सूर्याला पूर्णपणे झाकू शकतो. त्यालाच 'ग्रहण' करतो म्हणता येईल. पण शुक्र फार लहान असल्याने त्याने सूर्य ग्रहण केलं असं म्हंटलेलं बरोबर वाटत नाही. उलट सूर्यानेच त्याचं 'ग्रहण' केलं असं दिसतं. म्हणून शुक्र सूर्य युती असं लेखात म्हंटलेलं आहे.
तळटीप [५] :- युतीचा उपयोग
--------------------------------
लांब वरच्या तार्यांना ग्रह आहेत की नाहीत हे दुर्बिणीतून नुसतं बघून कळत नाही, कारण एकच! अंतर! त्यामुळे त्याच्या भोवती काही फिरतं आहे की नाही हे त्या तार्याकडून येणार्या प्रकाशाच्या तीव्रतेत पडणार्या फरकावरून समजू शकतं. तार्याच्या समोरून त्या तार्याचा एखादा ग्रह जेव्हा जातो तेव्हा आपल्याला त्या तार्याकडून येणारा प्रकाश थोडा मंद झालेला दिसतो, फार जास्त नाही पण थोडा! उदा. गुरू सूर्यासमोरून गेला तर सूर्याची तेजस्विता फक्त सुमारे १% ने कमी होईल. याचा वापर करून त्या तार्याभोवती कुणी फिरतं आहे की नाही ते ठरवता येतं.
काही शास्त्रज्ञांची तोंडओळख
-------------------------------
१> केप्लर(१५७१-१६३०) : टायको ब्राहे या १६व्या शतकातील खगोल शास्त्रज्ञाने खूप मेहनतीने ग्रहांच्या कक्षा व तार्यांच्या जागा मोजून लिहून ठेवल्या होत्या. त्याला त्या माहिती वरून सूर्यमालेची प्रतिकृती बनवायची होती. त्यासाठी त्यानं केप्लर नावाच्या एका हुशार मुलाला आपला मदतनीस म्हणून नेमला. १६०१ मधे ब्राहेचं निधन झाल्यावर त्या माहितीचा वारसा केप्लरकडे चालत आला आणि त्यानं तेच काम पुढे चालू ठेवलं. ब्राहेने वापरलेली यंत्रं आणि मोजमाप पद्धती जास्त अचूक असल्यामुळे त्या माहितीतून केप्लरला इतरांना सहज न दिसलेल्या गोष्टी समजल्या. त्यातूनच त्याचे ३ नियम प्रसिद्ध झाले. या लेखात दिलेलं समीकरण हा त्याचा तिसरा नियम आहे आणि प्रथम ८ मार्च १६१८ रोजी त्याला तो सुचला हे त्यानंच त्याच्या 'द हार्मनी ऑफ द वर्ल्ड' या पुस्तकात नमूद केलं आहे.
२> एडमंड हॅली(१६५६-१७४२) : हॅली एक अत्यंत हरहुन्नरी माणूस होता. जहाजाचा कप्तान, नकाशे बनविणारा, ऑक्सफर्ड विद्यापीठातला भूमितीचा प्राध्यापक, डेप्युटी कंट्रोलर ऑफ रॉयल मिंट, खगोल शास्त्रज्ञ इ. इ. त्याची ओळख अशी विविध पदरी आहे. धूमकेतूला त्याचं नाव दिलं आहे पण शोध त्यानं लावला नाही. त्यानं फक्त १६८२ साली आलेला धूमकेतू आणि १४५६, १५३१ व १६०७ साली येऊन गेलेले धूमकेतू एकच आहेत आणि त्याची कक्षा कशी आहे इतकंच सांगितलं . पण त्या धूमकेतूला 'हॅलीचा धूमकेतू' हे नाव त्याच्या मृत्यू नंतर १६ वर्षांनी मिळालं. दर ७६ वर्षांनी येणारा हा धूमकेतू बहुतेकांच्या आयुष्यात फार तर एकदाच तोंड दाखवतो. उभ्या आयुष्यात हा धूमकेतू दोनदा येऊन जाण्याची शक्यता तशी कमीच! हे भाग्य मार्क ट्वेन ला लाभलं होतं. तो जन्माला आला आणि मृत्यू पावला त्या दोन्ही वर्षी धूमकेतू आकाशात होता.
संदर्भ/क्रेडिट्स :-
------------------
१) आकृत्या खालील स्थळांवरील आहेत!
अ> http://spiff.rit.edu/classes/phys235/venus_t/venus_t.html
ब> http://www.sciencebuddies.org/science-fair-projects/project_ideas/Astro_...
क> http://www.exploratorium.edu/venus/P_question4.html
२> Coming of age in the milky way. By Timothy Ferris.
३> A short history of nearly everything. By Bill Bryson.
४> Article by Trudy Bell: http://www.tbp.org/pages/publications/bent/features/su04bell.pdf
-- समाप्त --

धन्यवाद! 'जड आहे बरचंसं' असं
धन्यवाद! 'जड आहे बरचंसं' असं काही जणांना वाटतंय, पण त्यात खरं तर शाळेतल्या भूमिती शिवाय पेक्षा काहीच जड नाहीये. आणि तितकी प्रत्येक जण शिकलेला असतो असा माझा समज आहे, किंवा होता म्हणू या आता!
अर्थात अशा प्रतिक्रिया येणार याची पूर्ण कल्पना होती, म्हणून काही गोष्टी मुद्दाम तळटीपेत टाकल्या आहेत. मुख्य मुद्दा असा की लेख जड वाटला तरी युती बघायला विसरू नका!
भारी लेख! चिमण, तू आता लवकर
भारी लेख!
चिमण, तू आता लवकर एखादा नवीन धूमकेतू शोधून काढ. त्या धूमकेतूला तुझं नाव मिळेल.
छान माहिती, नकाशा तर जबरदस्त
छान माहिती, नकाशा तर जबरदस्त आहे. आता ६ जुनला वरूणदेव प्रसन्न होऊन त्यांच्या घरीच बसले तर बर होईल

आमच्या गावात, आमच्याच
आमच्या गावात, आमच्याच रस्त्यावर जून ५ ला संध्याकाळी ६ वाजून ३ मिनिटे ते ६ वाजून २१ मिनिटे पर्यंत सूर्यासमोर नुकताच येत असलेला शुक्राचा काळा ठिपका दिसेल, पण अगदी सूर्याच्या मधे तो रात्री ९ वाजता येतो, तोपर्यंत सूर्य घरी गेलेला असतो. म्हणजे शुक्र दिसेल, पण बहुतेक नेहेमी सारखा. कदाचित नाही पण, सूर्याचा प्रकास त्याच्यावर पडल्याने दिसणार पण नाही.
श्रीकृष्णाचा धावा केला नि सांगितले की जयद्रथाला मारायचे आहे, तर तो कदाचित अस्ताला गेलेला सूर्य परत आकाशात आणेल. किंवा नुकतेच देवोंके देव महादेव या सिरियलमधे चंद्राचे प्राण वाचवता यावेत म्हणून नंदी की शिव सूर्यास्त करण्यास विलंब करतो असे आठवते (एव्हढे बारकावे काही लक्षात रहात नाहीत खरे म्हणजे) .
आय टी मधल्या लोकांना जसे रात्रीपर्यंत फुकट डांबून ठेवता येते, तसे त्या दिवशी तरी सूर्याला डांबून ठेवता आले रात्री १२ वाजेस्तवर तर बरे होईल.
खूप धन्यवाद. अधिकाधिक हवे.
खूप धन्यवाद. अधिकाधिक हवे.
खुप माहीतीपुर्ण लेख धन्यवाद
खुप माहीतीपुर्ण लेख
धन्यवाद
१ ए यु म्हणजे नेमकं किती ?
१ ए यु म्हणजे नेमकं किती ?
अफाट! मजा आली वाचताना. 'ब्रीफ
अफाट! मजा आली वाचताना. 'ब्रीफ हिस्ट्री ऑफ ऑलमोस्ट एव्हरीथिंग'ची आठवण झाली.
याचा इतिहास बघताना तेव्हाचं सर्वच विषयातलं तोकडं ज्ञान, ते ज्ञान वाढवण्याचा ध्यास घेतलेले शास्त्रज्ञ, त्यांचं चातुर्य व कल्पकता, त्यांचे कष्ट व धडपड, आलेल्या अनंत अडचणी, त्यातून मार्ग काढण्यासाठी दाखवलेली जिद्द तसंच त्या वेळची अपुरी, तुटपुंजी व बाल्यावस्थेतील साधन सामुग्री या असंख्य गोष्टी समोर येतात>>> असं काही नसतं हो, आपल्या पोथ्या-पुराणात हे सगळं आधीच कूट भाषेत लिहून ठेवलेले होते, पाश्चात्यांनी ते चोरुन नेले व त्यांचे म्हणून सांगितले, इतकं सोप्पं आहे हे सगळं!!!!!!!!!!
घरातल्या एकमेव खगोलप्रेमीनं
घरातल्या एकमेव खगोलप्रेमीनं अगदी आवडीनं सगळं वाचून काढलं, चित्रं, नकाशे, अॅनिमेशन, जे-जे काही दिलेलं आहे, ते सगळं अभ्यासलं
पुनश्च धन्यवाद सर्वांना! >> १
पुनश्च धन्यवाद सर्वांना!
>> १ ए यु म्हणजे नेमकं किती ?
जादुगरा, लेखात खालील वाक्य आहे...
शेवटी, १९६४ साली १ AU म्हणजे ९२, ९१०, ००० +/- १२५० मैल इतकं अंतर अशी घोषणा इंटरनॅशनल अॅस्ट्रॉनॉमिकल युनियनने केली.
हा प्रश्न मला सर्व रामायण ऐकल्यावर 'रामाची सीता कोण' सारखा वाटला.
>> घरातल्या एकमेव खगोलप्रेमीनं अगदी आवडीनं सगळं वाचून काढलं
लले हे इथे मुद्दाम सांगितल्याबद्दल प्रचंड धन्यवाद! लेख लिहीण्यासाठी घातलेला वेळ सार्थकी लागला माझा! आता युती नक्की बघा
>> पाश्चात्यांनी ते चोरुन नेले व त्यांचे म्हणून सांगितले
नशीब त्यामुळे तरी आपल्या पोथ्या-पुराणात काय काय होतं ते समजतंय!
२००४ सालची युती आम्ही भिंतीवर
२००४ सालची युती आम्ही भिंतीवर इमेज प्रोजेक्ट करून अगदी सविस्तर पाहिली होती. योग्य जागी आणि योग्य अँगलने दुर्बिण सेट करणे, वगैरे गोष्टी घरातल्या एकमेव शास्त्रज्ञाने सकाळी ऑफिसला जाण्यापूर्वी करून ठेवलेल्या होत्या. नंतर दिवसभर दुर्बिण थोडी थोडी हलवणे इ. सोपी कामं मी केली. सोसायटीतली तमाम बाळगोपाळ मंडळी येऊन डोकावून गेली होती.
हा नकाशाही पहा:
हा नकाशाही पहा: http://www.sunaeon.com/venustransit/
केपलराय नम:! चिमणाय नमः!
केपलराय नम:! चिमणाय नमः! आशिषाय नमः!
प्राथमिक वाचन केले. त्यावरून बरेचसे समजले. समजावून देण्यासाठी (फार अवघड काम!) दिलेल्या आकृत्यांमुळे समजायला फार मोठी मदत होते. पण कांही भाग नीट समजायला पुन्हा वाचणार आहे.
या सकस लेखाबद्दल धन्यवाद!
>>जॉन हॅरिसन नावाच्या एका अशिक्षित सुताराने तसं घड्याळ बनवण्याचा ध्यास घेतला. आयुष्यातली जवळपास तीसेक वर्ष खर्ची घालून त्यानं विविध व वेगवेगळ्या अचूकतेची घड्याळं बनवली. त्याचं एक घड्याळ, १७६१ साली, एच. एम. एस. डेप्टफर्ड या जहाजावरून पोर्ट रॉयल जमैका येथे पोचेपर्यंत त्याच्यावरची वेळ फक्त ५.१ सेकंदांनी चुकली होती>>
ग्रीनविच (ग्रिनिच), लंडन येथिल संग्रहालयात त्याने तयार केलेले घड्याळ आणि त्याबद्दलची माहिती पाहिल्याचे थोडे आठवते. तेथे खूपच निरनिराळी जपून ठेवलेली उपकरणे आहेत. ते संग्रहालय आणि त्यातील उपकरणांबद्दल असलेली माहिती खूपच चांगली आहे. नीट पाहायचे तर पूर्ण दिवस हवा.
उद्या बघायला विसरु
उद्या बघायला विसरु नका.
कॅलटेकच्या वेब साईटवर काही चांगल्या लिंका आहेतः http://www.astro.caltech.edu/outreach/VenusTransit/
लोक ट्रांझीट पहायला कॅलटेकला येऊ शकतात. RSVP आवश्यक.
ट्रांझिट ऑफ व्हीनस. चा
ट्रांझिट ऑफ व्हीनस. चा वेबकास्ट पण होणार आहे. नेहरू प्लॅनेटेरिअमच्या साइट वर उपलब्ध आहे. माहिती पण आहे. पुढील ट्रांझिट २११७ मध्ये.
या ठिकाणी, मराठीत
या ठिकाणी, मराठीत अधिक्रमणाबद्दल रंजक भाषेत माहिती दिलेली पीडीएफ आहे.
मूळ लेखक - नीरज मोहन, National Centre for Radio Astrophysics
भाषांतर - मिहीर अर्जुनवाडकर
या ठिकाणी पब्लिक प्रोग्रॅम्स कुठे आहेत याचीही माहिती मिळेल.
http://transitofvenus.nl/wp/where-when/local-transit-times/
मुंबई आणि आजूबाजूच्या भागात खगोल मंडळ या संस्थेने शिवाजी पार्कात जाहीर कार्यक्रम आयोजित केला आहे. तिथे दुर्बिणीचे प्रोजेक्शन वापरून, फिल्टरशिवाय अधिक्रमण पहाता येईल, असे त्यांच्या इमेल/फेसबुकावरून समजले.
http://www.khagolmandal.com/ या त्यांच्या संस्थळावर अधिक माहिती आहे.
बरं झालं ही लिंक दिलीस.
बरं झालं ही लिंक दिलीस. दुपारी मराठी पिडीएफ ची लिंक काम करत नव्हती.
हॅ हॅ हॅ ... एन.सी.आर.ए.च्या
हॅ हॅ हॅ ... एन.सी.आर.ए.च्या आतल्या जगातल्या लिंका न चालणं ही फार दुर्मिळ घटना नाही.
विसरु नका! २ तासांनी पहिला
विसरु नका! २ तासांनी पहिला कॉण्टॅक्ट
ओरलँडोत ढग्....पाऊस!
ओरलँडोत ढग्....पाऊस!
बघणार नक्की! मित्राच्या
बघणार नक्की! मित्राच्या कृपेने गॉगल ही मिळालाय स्पेशल .. तेव्हा दोन तासांनीं दर्शनाचा लाभ घेणार ..
न्यू इंग्लंडात पण नॅसाच्या
न्यू इंग्लंडात पण नॅसाच्या साईटवर वेबकास्ट आहे. बघणार.
नॅसाच्या साईटवर वेबकास्ट आहे. बघणार.
वेबकास्ट पहात असाल तर पहिला
वेबकास्ट पहात असाल तर पहिला कॉण्टॅक्ट चूकवु नका.
दिसायला लागलं का? मी आता
दिसायला लागलं का? मी आता बघायचा प्रयत्न केला पण काहीच दिसलं नाही .. :|
हो. दिसायला लागलं. प्रत्यक्ष
हो. दिसायला लागलं. प्रत्यक्ष बघून नाही का दिसत? इथे बघा..
http://venustransit.nasa.gov/transitofvenus/index_akamai.php
अगं मृ, त्या गॉगलने बघत होते
अगं मृ, त्या गॉगलने बघत होते .. आता परत जाऊन बघते ..
http://www.guardian.co.uk/sci
http://www.guardian.co.uk/science/2012/jun/05/transit-of-venus-live-cove...
इथे पण बघा.
तो स्पॉट वरच्या बाजूला आहे की
तो स्पॉट वरच्या बाजूला आहे की खालच्या ..
ह्याहीवेळेला नीट काही दिसलं नाही आणि थोडा वेळ टक लावून बघितलं की उगीच सगळीकडेच स्पॉट्स दिसायला लागतायत .. :p
दिसला, ठिपका दिसला!
दिसला, ठिपका दिसला!
सशल, साधारण 8 O' clock .
सशल, साधारण 8 O' clock .
Pages