सौंदर्यलक्ष्यी रामानुजन

तुम्ही गणित करता म्हणजे काय करता बरं? असा प्रश्न मला नेहमी लोक विचारतात. 'आता कुठले प्रश्न राहिलेत सोडवायचे बुवा?' असं प्रश्नचिन्ह भल्याभल्यांच्या चेहर्‍यावर उमटलेलं दिसतं. "Τι κάνεις όταν κάνεις μαθηματικά;" अर्थात 'जेव्हा तुम्ही गणित सोडवता तेव्हा काय करता' असा ग्रीक भाषेत प्रश्न २५०० वर्षांपूर्वी युक्लिडलाही विचारत होते म्हणे. "तात, त्वं गणिते किं करोषि?" असा प्रश्न भास्कराचार्यांनी लीलावतीच्या बाळमुखातून ऐकला असल्याचे कळाल्यास मला नवल वाटणार नाही. पण गंमत अशी, की गणितज्ञांनीही हा प्रश्न हर्षोत्फुल्ल आश्चर्याने विचारावा असा एक गणितज्ञ इये भारतवर्षी होऊन गेला, तो म्हणजे श्रीनिवास रामानुजन. 'मित्रा, तू हे असं कसं करू शकतोस बरं?' असं ज्याला काहीशा अंमळ कौतुकमिश्रित लटक्या रागाने खांद्याला धरून विचारावं असा हा निखळ प्रतिभावान माणूस. हा ह्या भारतात होऊन गेला, हे भारतातल्या आम्हा गणितज्ञांच्या दृष्टीने भाग्यच, पण भारतातल्या लोकांना फक्त नामघोष करायची सवय असल्याने 'बुवा हा एक रामानुजन की कायसासा तो होऊन गेला' ह्यापलीकडे रामानुजनबद्दल आपल्याला काय माहिती आहे, ह्याचा आपण कधी विचार केला आहे का?

अनेक गणितज्ञांना रामानुजनच्या प्रतिभेने वेडावून टाकलं होतं. हा माणूस अदमासे सव्वाशे वर्षांपूर्वी ब्रिटिश साम्राज्याच्या कुठल्या एका कोपर्‍यात म्हणता येईल अश्या एरोड, कुंभकोणम वगैरे तामिळनाडूमधल्या भागात वाढला. त्याची १८९०च्या दशकामधली कुठली तमिळ शाळा आहे ती, आणि माझी १९९०च्या दशकामधली मराठी शाळा, दोन्ही दिसायला अगदी सारख्या! त्यामुळे माझ्यासारख्या मुलाला तर त्याचं अजूनच अप्रूप वाटतं. हा माणूस अतिशय प्रगत वगैरे शहरात गणितज्ञांच्या नावाजलेल्या कुटुंबात वगैरे जन्मला असता, तरी त्याने घेतलेली सूर्याकडे झेप डोळे दीपवणारीच असती. पण हा एका निम्न मध्यमवर्गीय घरात वाढला. अश्या भागात वाढला, की जिथे वर्षानुवर्षांच्या अनास्थेने परिस्थिती अशी झाली होती, की ह्याचं डोळे दीपवणारं विश्वरूप बघण्याची शक्ती असलेला संजयसुद्धा पैदा झाला नव्हता!

तुम्हाला वाटत असेल, की मी अतिशयोक्ती करतोय. पण केंब्रिज, ऑक्सफर्डसारख्या विद्यापीठात मानाची प्राध्यापकपदं भूषविलेला विसाव्या शतकातला मोठा इंग्लिश गणितज्ञ जी. एच. हार्डी ह्याला जेव्हा विचारण्यात आलं, की गणितामध्ये तुझं सर्वोत्तम योगदान काय असेल? तेव्हा त्याने उत्तर दिलं, "मी रामानुजनचा शोध लावला"! बरं, हार्डी कोणी असातसा नव्हता. तो स्वतः २-३ वर्षांचा असताना कोटींच्या घरातल्या संख्या लिहून त्यांची बेरीज करायचा असा बालगणिती होता. रिमान हायपोथेसिस सारख्या १५० वर्षांपासून न सुटलेल्या प्रश्नावर हार्डीचं महत्त्वाचं काम झालं होतं. अमूर्त गणिताचा खुंटा इंग्लंडमध्ये बळकट करण्यात हार्डीचा सिंहाचा वाटा होता. अश्या जबर माणसालासुद्धा वेड लागावं, अशी रामानुजनची प्रतिभा होती!

त्याला कारणच तसं होतं. रामानुजनच्या हाती शाळेत १५-१६ वर्षांचा असताना जॉर्ज कारचं गणिती सूत्रांचं पुस्तक लागलं. ह्यात फक्त सूत्रं होती, पण ती कुठून आली, का आली, कशी आली, ह्याविषयी काही विवेचन नव्हतं. 'चक्कू ताड्या घोटा' अशी नुसती पाठांतरसंस्कृती वाढीस लागलेल्या देशात त्याची काही गरजही नव्हती, असा विचार खेदाने मनात येतो. पण रामानुजन पठ्ठ्या त्यावर थोडीच स्वस्थ बसणार! पुढच्या ४-५ वर्षांत रामानुजनने प्रत्येक सूत्राचा प्रत्येक पेच तपासून बघितला. खास भारतीय पद्धतीने तो पाटी-पेणसल घेऊन बसायचा, प्रत्येक सूत्र कसं आलं ते शोधायचा, त्याची सिद्धता लिहायचा. असे सहा हजार सिद्धांत आणि सूत्रे त्याने स्वतः सिद्ध केली. हे असं सांगून त्याच्या ह्या भीमकाय कामाविषयी नीट कळणार नाही. जर एखाद्या १५-१६ वर्षांच्या मुलाला तुम्ही चांद्रयान नुसतं दाखवलंत आणि त्याने ते स्वतः उघडून स्वतःहून शोधून काढलं, की त्याची ज्वलनप्रणाली आणि यंत्र कसं चालतंय, मग त्याने न्यूटनचा गुरूत्वाकर्षणाचा नियम, बर्नौलीचे द्रवगतीचे नियम हे सगळं शोधून त्यायोगे यानाची गती किती असली पाहिजे वगैरे बरोब्बर निदान काढून दाखवलंन, आणि ह्या सगळ्यात इतर कोणाचीही मदत नाही, तर किती मोठा धक्का बसेल, तसा धक्का हे ऐकल्यावर बसतो!

मुळात रामानुजनने २००० वर्षांपासून मानवाला गणितामध्ये वेगवेगळ्या गणितज्ञांमुळे जे ज्ञान प्राप्त झालं होतं, ते सगळं एकट्याने पुनर्साध्य करून दाखवलं. वास्तविक त्याला हे करायची गरजच नव्हती. त्रिकोणमितीचे नियम वगैरे हजारो वर्षांपासून माहिती होते. पण हे रामानुजनला माहितीच नव्हतं. ब्रिटिशांच्या साम्राज्यात पिचलेल्या भारतात जन्माला यायची ही शिक्षाच होती. असं होऊ नये म्हणूनच देशोदेशीच्या गणितज्ञांचा आणि शास्त्रज्ञांचा एकमेकांशी संपर्क यायला हवा. ते एकत्र यायला हवेत. देशात परिषदा व्हायला हव्यात. ज्ञानाचा मार्ग सुलभ व्हायला हवा. अर्थात हे आजच्या भारतातसुद्धा होणं मुश्किल झालं आहे, तर तेव्हा काय होणार होतं? पण रामानुजनसारखा स्वयंप्रज्ञ माणूस म्हणून गप्प बसणार्‍यातला थोडीच होता? त्याने हे सगळं ज्ञान स्वतःच शोधून काढलं! बरं, हे करताना त्याच्या लक्षात आलं, की आपल्याला ह्या पुस्तकात नसलेल्या गोष्टीसुद्धा सुचतायत! मग त्याने ह्या सगळ्या गोष्टी लिहून काढायला सुरवात केली. पण ह्याचं कुटुंब पडलं गरीब. कागद विकत घ्यायला तरी कुठला पैसा? त्यामुळे ह्याने फक्त सुचलेली सूत्रं लिहून ठेवली. त्यांनीच ५-६ जाडजूड वह्या भरल्या. ह्या वह्यांतल्या सूत्रांची सिद्धता करण्याचं आणि त्यांच्यातलं सौंदर्य शोधायचं काम आज १०० वर्षांनंतरही संपलेलं नाही!

रामानुजनची कल्पनाशक्ती काय अचाट होती, आणि इतर गणितज्ञांनाही तो कसा चकित करून सोडत असे, हे समजण्यासाठी उदाहरणादाखल छोटी गोष्ट सांगतो. कोलकात्याच्या इंडियन स्टॅटिस्टिकल इन्स्टिट्यूटचे संस्थापक पी. सी. महालनोबिस आणि रामानुजन समकालीन होते. केंब्रिजमध्ये हे दोघे काही काळ एकत्र होते. एकदा रामानुजनच्या घरी असताना महालनोबिस एक कोडं सोडवत होता. त्याने बराच वेळ विचार करून ते सोडवले, तेव्हा रामानुजन स्वयंपाकघरात चुलीवर रसम ढवळत होता. महालनोबिस त्याला म्हणाला, "आज मी एक मस्त कोडं सोडवलंय. तुला विचार करायचा का त्यावर?" रामानुजन काम करता करताच म्हणाला, "बोल की!" ह्यावर महालनोबिसने सांगितलेले कोडे पुढीलप्रमाणे -

एका रस्त्यावर ५० ते ५०० च्या दरम्यान संख्येने काही घरे आहेत. घरांचे क्रमांक १ पासून सुरू होऊन १, २, ३, ... असे क्रमाने वाढत जातात. ह्या रस्त्यावर घर क्र. १ पासून सुरवात करून चालता चालता एका घरापाशी आल्यावर असे लक्षात येते, की त्या घराच्या डावीकडे असलेल्या घरांच्या क्रमांकांची बेरीज आणि त्या घराच्या उजवीकडे असलेल्या घरांच्या क्रमांकांची बेरीज समान आहेत! (दोन्ही बेरजांत त्या घराचा क्रमांक धरलेला नाही.) तर त्या घराचा क्रमांक आणि घरांची एकूण संख्या सांगा.
महालनोबिसला स्वतःला हे करायला बराच वेळ लागला होता. पण आश्चर्याची गोष्ट म्हणजे अगदी हे कोडे सांगताक्षणीच रामानुजन उद्गारला, "घे उत्तर लिहून!" आणि त्याने महालनोबिसला असे एक सूत्र सांगितले, की त्याने ५० ते ५००च काय, पण त्या कक्षेबाहेरीलही सर्व अगणित उत्तरे मिळतील! महालनोबिस ह्यावर हतबुद्ध होऊन पाहत राहिला!

उत्तराबद्दल विचार कसा करावा, ह्याबद्दल थोडा साधा विचार करू. –

जर घरांची एकूण संख्या m मानली, व त्या घराचा क्रमांक n मानला, तर आपल्याला पुढील समीकरण हवे आहे -

थोडीफार बेरीज-वजाबाकी करून ह्या समीकरणास पुढील रूप देता येते -

ह्यात थोडं नवीन नामकरण करून ह्याला आपण जरा सोपं करू.

आणि मग आपल्याला मिळेल ते सुप्रसिद्ध 'ब्रह्मगुप्त-पेल समीकरण' -

अर्थात, ह्या समीकरणाच्या आपल्याला पूर्णांकांत उकली शोधायच्या आहेत, म्हणजे x आणि y हे दोन्ही पूर्णांकच असले पाहिजेत.
आता काय विचार करावा? समजा वरील समीकरणाऐवजी आपल्याला त्यात १ ऐवजी ०, म्हणजे अगदी थोडासाच बदल करून मिळालेले पुढील समीकरण सोडवता येईल का?

तर हे समीकरण पूर्णांकांत सोडवता येणार नाही. कारण हेच समीकरण आपण पुढीलप्रमाणे पुनर्लिखित करू शकतो -

म्हणजेच,

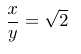
पण आपल्याला माहिती आहे, की २ चे वर्गमूळ अश्या प्रकारे पूर्णांकांच्या भागाकाराच्या रूपात लिहिता येत नाही, कारण ते अपरिमेय आहे.

पण काही हरकत नाही! हे नवीन समीकरण सोडवता येत नाही तर नको येऊ दे! आपलं मूळ समीकरण (*) सोडवता येणार नाही, असं कोणीच म्हटलेलं नाही. पण ह्या समीकरणात आणि मूळ समीकरणात थोडासाच फरक आहे, ह्याचाच अर्थ आपल्या मूळ (*) समीकरणाचं उत्तर x आणि y असेल, तर हा भागाकार २ च्या वर्गमूळाच्या जवळचा असला पाहिजे! अर्थात, आपल्याला असे दोन पूर्णांक हवेत, ज्यांचा भागाकार २ चे वर्गमूळ तर नाही, पण त्याच्या जवळ जाणारी संख्या असेल. म्हणजे मग आपल्याला x आणि y, व त्यायोगे m आणि n मिळतील.

रामानुजनने हा सर्व विचार क्षणार्धात केला आणि २ च्या वर्गमूळाच्या जवळ जाणार्‍या संख्या शोधायला सुरवात केली. अश्या काही संख्या पुढीलप्रमाणे होत -

१/१, ३/२, ७/५, १७/१२, ४१/२९, ९९/७०, २३९/१६९, ...

ह्या संख्या यादृच्छिक अजिबात नाहीत. तुम्ही थोडंसं ह्यांकडे टक लावून पाहिलंत, तर लक्षात येईल, की आधीच्या संख्येतल्या अंश आणि छेदाची बेरीज हा पुढच्या संख्येचा छेद आहे! (१+१ = २, ३+२ = ५, ७+५ = १२, १७ + १२ = २९, ...) अर्थातच ह्यामागे काहीतरी आशय दडलेला आहे. थोडा अजून विचार केलात, तर दिसेल, की ह्या नवीन छेदात आधीचा छेद अजून एकदा मिळवलात, की नवीन अंश तयार होतो! (२+१ = ३, ५ + २ = ७, १२ + ५ = १७, २९ + १२ = ४१, ...) एकंदरीतच काहीतरी गौडबंगाल आहे की इथे! एक सुंदर रचनाक्रम दिसतो आहे. अगदी भरगच्च पानांच्या गुच्छात गंधित फुलं दडलेली असावी आणि आपण त्यांना हुडकून काढून सुगंध घ्यावा, आणि त्यांना प्रेमभराने न्याहाळावं तशी परिस्थिती. 'गणित म्हणजे आकडेमोड' असा समज मोडून काढणारा हा आकृतीबंध. संगीत निर्माण करणं म्हणजे काही नुसतं जाऊन पेटीवरच्या वाट्टेल त्या कळा वाट्टेल तश्या दाबणे, असं नसतं. गणिताचंही तसंच आहे. आकड्यांमध्ये म्हणा किंवा आकृत्यांमध्ये म्हणा, अश्या दडलेल्या खुब्या असतात, त्या शोधून काढाव्या लागतात. त्यांच्याशी बोलावं लागतं. आकड्यांना कधी हळुवार गोंजारून त्यांच्या मनातलं गुपित काढून घ्यावं लागतं. थोडा वेळ त्यांच्याबरोबर घालवला, की मगच त्या तुमच्यासाठी दार उघडतात.
आता असे आकृतीबंध बघायला, निर्माण करायला सौंदर्यदृष्टी असणं गरजेचं आहे. ज्ञानेश्वर म्हणतात तसं अरूपाला सरूप देण्याचाच हा प्रकार. संगीतातल्या सप्तसुरांच्या विविध आकाराच्या लाटा बनवून संगीत दिग्दर्शक आणि गायक आपल्याला कसे त्यावर समुद्राची सैर करून आणतात, तसंच गणिताचं आहे खरंतर. सगळेच संगीत दिग्दर्शक होऊ शकत नाहीत, पण म्हणून त्यातल्या गोडीपासून आपण वंचित राहत नाही हेही खरंच. पेढा खाता यायला हलवाई होण्याची गरज नाही. संगीत दिग्दर्शक होण्यासाठी म्हणा किंवा हलवाई होण्यासाठी म्हणा, जी काय सौंदर्यदृष्टी असेल ती काही लोकांकडे उपजत असते, काही लोकांना हळूहळू मिळते. तसंच गणिताचं आहे, पण आपल्याला हे सगळं न होताही गणिताचा आस्वाद घेता येऊ शकतो, हे आधी ध्यानात घ्यायला हवं, आणि मग अशी दृष्टी ज्यांना मिळाली आहे, त्यांच्या कलेचा आणि प्रतिभेचा आस्वाद खुल्या दिलाने घेत रहावा.

ह्या विचारावर आपल्याला रामानुजनचं मोठेपण कळायला सुरवात होते. रामानुजन गणिताच्या तंत्रामध्ये तर मुरलेला होताच, पण त्याला गणिताचा जो मंत्र गवसला होता, त्याची मोहिनी गणितातल्या भल्याभल्या जादूगारांना पडली होती आणि आहे. गणितात अनंत प्रश्न आणि अनंत संभाव्यता असतात, पण नक्की काय केलं असता सर्वात खुमासदार गोष्ट घडेल, नक्की काय केलं असता प्राजक्ताचं टपोरं फूल अलगद आपल्या ओंजळीत येऊन पडेल हे कळण्याची रामानुजनची प्रज्ञा वादातीत आहे. ज्याला 'aesthetic sense ' म्हणता येईल, तो रामानुजनकडे सर्वोत्तम भरला होता. अहो, ह्याने मद्रासमध्ये कारकून म्हणून काम करत असताना त्याच्या अर्ध्या शतकापूर्वी बर्नार्ड रिमानने जे झीटा फल शोधून काढून त्याचे महत्त्वाचे गुणधर्म शोधले ते स्वतःहून शोधले हो. हार्डीला लिहिलेल्या पत्रात त्याने ते अभिमानाने लिहिले. ते पाहून हार्डीला काय वाटलं ते त्याने लिहून ठेवलं आहे. बालमोझार्टकडे तो पियानो वाजवून सुरेल सुरावटी ऐकवत असताना कौतुकाने पाहावं, तसं त्याने लिहिलं आहे. त्याचं कारणच तसं आहे. हा रिमान म्हणजे जर्मनीमधल्या गणितज्ञांचा शिरोमणी होता. गॉटिंजनसारख्या अग्रगण्य विद्यापीठात तो नवनवीन विषयांची मुहूर्तमेढ रोवत होता. गॉस, डेडेकिंड, डिरिश्ले, अश्या मोठ्या गणितज्ञांच्या माळेतला हा पुढचा मणी होता. अश्या परंपरेतून पुढे आलेल्या तेजाची बरोबरी रामानुजनने एकट्याच्या जोरावर करून दाखवली म्हणा ना! त्याची प्रतिभा इतकी उच्चीची होती, की ती जाणून घ्यायलासुद्धा हार्डीसारखा रसिक लागला. संगीतातले सात सूर सगळ्यांनाच माहिती असतात, अनेकांना त्यात गतीही प्राप्त होते, पण ते काहींचेच सख्खे मित्र होतात. गणितातले अंक रामानुजनचे असेच जीवाभावाचे मित्र होते. त्यामुळे त्याला जी सौंदर्यदृष्टी लाभली, त्यासी तुळणा नसे, तुळणा नसे ...

रिमानच्या आधीचा मोठा गणिती म्हणजे त्याचाच पीएचडी मार्गदर्शक, गणिताचा राजकुमार म्हणवला जाणारा कार्ल फ्रिडरिख गॉस. गॉसच्या क्लास नंबर प्रॉब्लेममधून निर्माण होणारी नित्यसमीकरणे रामानुजनने स्वतःहून शोधून काढली. ऑयलर आणि गॉससारख्या गणितज्ञांनी अभ्यासलेली हायपरजॉमेट्रिक सिरीज रामानुजनने पुनरुज्जीवित केली. त्यातून त्याने 'पाय' साठी अनेकोत्तम सूत्रे शोधून काढली. ह्यासाठीच काही जण त्याला 'पाय'चा राजकुमार म्हणतात. त्याच्या पत्रातील हायपरजॉमेट्रीक सिरीज हार्डीला गॉसच्या इंटीग्रल्सपेक्षाही जास्त महत्त्वाची वाटली. आजही अल्जिब्राईक नंबर थिअरीमध्ये ह्याचा अभ्यास अतिशय महत्त्वाचा ठरतो.

वरच्या कोड्यात जी उत्तरं आहेत, ती रामानुजनच्या अश्याच एका आवडीच्या विषयातून येतात. त्याचं नाव 'कंटिन्यूड फ्रॅक्शन्स' अर्थात 'निरंतर अपूर्णांक'. त्यांच्यावरचे थिअरम्स रामानुजनच्या हार्डीला लिहिलेल्या पहिल्यावहिल्या पत्रात शेवटच्या पानावर होते. ते पाहून हार्डीची अवस्था 'मी हातातली शस्त्रे खाली टाकतो' अश्यासारखी झाली, असं त्याने लिहून ठेवलंय. हार्डीने रामानुजनच्या पत्राला उत्तर द्यायचं का ठरवलं, ह्यावर त्याचं उत्तर मोठं मार्मिक आहे. तो म्हणतो, "मी हे थिअरम्स बघून हतबुद्ध झालो. ते सिद्ध कसे करावेत हे तर सोडाच, पण ते खरे आहेत का हे तरी कसं ओळखावं? मी ह्यासारखं काहीच आजवर कधी बघितलं नव्हतं. पण हे थिअरम्स खरे असलेच पाहिजेत, कारण ते खरे नसताना नुसतंच दडपून देण्याची कल्पनाशक्तीच मुळी कोणातच असणं शक्य नाही!" एका जाणकार आणि तरबेज गणितज्ञालासुद्धा गोंधळून टाकणारी ही करामत, ह्यास अजून मोठ्या प्रशस्तीपत्रकाची काय गरज असू शकते?

हे इतकं सगळं आधीच करून झालं होतं. मग रामानुजन केंब्रिजला गेला. तिथे त्याला अजूनच बहर आला. हार्डी, लिटलवूड अश्या तोडीच्या गणितज्ञांबरोबर रामानुजनने त्याचं स्वतःचं असं मोठं पहिलं काम केलं ते पार्टिशन फलांवर. समजा 'न' ही नैसर्गिक संख्या असेल, तर न चे किती प्रकारे भाग पाडता येऊ शकतात? असा हा प्रश्न. ती संख्या म्हणजे P(न). उदाहरणार्थ,

४ = १ + ३
४ = १ + १ + २
४ = १ + १ + १ + १
४ = २ + २
४ = ४

म्हणून P(४) = ५. वरवर साधंसोपं वाटतंय हे. 'ह्या: काय भागच तर पाडायचेत' म्हणतील लोक. पण ही संख्या फार वेगात वाढते. उदाहरणार्थ

P(१००) = १९०, ५६९, २९२ (अबब!)

१०० चे भाग पाडायचे एकोणीस कोटी पाच लाख एकोणसत्तर हजार दोनशे ब्याणणव मार्ग आहेत! रामानुजनने त्याची 'सर्कल मेथड' शोधून काढली, आणि P(न) अगदी अचूक किंमतीपर्यंत शोधायचा अभिनव मार्ग शोधून काढला. आता तुम्ही म्हणाल, वर्तुळाचा आणि ह्या पार्टिशनचा काय संबंध?! पण तीच तर गंमत आहे. रामानुजनचा तो जागृत aesthetic sense इथे त्याच्या मदतीला आला. ह्याच सर्कल मेथडने नंतर व्हिनोग्राडोव्हने त्याची प्रसिद्ध वीक गोल्डबाख कंजेक्चरची सिद्धता दिली.
ह्या सर्कल मेथडला शंभर वर्षे आत्ता पूर्ण होतायत, त्यासाठी २०२० मध्ये जर्मनीमध्ये बॉनला परिषद आहे. रामानुजन असा कालातीत आणि अवस्थातीत होऊन भरला आहे म्हणा ना!

ह्याचबरोबर रामानुजनने ह्या पार्टिशन फलांच्या अनेक गुणधर्मांचा अभ्यास केला. उदाहरणार्थ, जर न चा शेवटचा अंक ४ किंवा ९ असेल, तर P(न) ह्या संख्येला ५ ने भाग जातो हे त्याने शोधून काढलं. (बघा करून!) मी जेव्हा पहिल्यांदा हे विधान पाहिलं, तेव्हा मला फार आश्चर्य वाटलं बुवा! 'काय संबंध आहे?' अशीच प्रतिक्रिया सगळ्यांची असते. पण एकदा नीट विचार करून ठाण मांडून ह्याचा अभ्यास केला, की मग ह्या असामान्य गणितज्ञाच्या प्रतिभेचा सुगंध एखाद्या राऊळात चाफ्याचा सुगंध दरवळावा तसा मनात दरवळतो. ह्या साध्याश्या विधानामागे जो गहन अर्थ दडला आहे, तो समजायला गणिताला ७०-८० वर्षांची प्रगती करावी लागली.

रामानुजनच्या सौंदर्यदृष्टीचं अजून एक उदाहरण. ह्या पार्टिशन फलाचं एक जनरेटींग फंक्शन म्हणून असतं. ते अभ्यासणं हा शतकांपासून चालत आलेला चोखाळलेला गणितज्ञांचा मार्ग. रामानुजनने एक गंमत केली. त्याने ह्या फंक्शनला फक्त खाली डोकं वर पाय करून, अर्थात क्ष ला १/क्ष करून लिहिलं. आणि त्यातून जन्माला आला रामानुजनचा डेल्टा मॉड्युलर फॉर्म! विसाव्या आणि एकविसाव्या शतकातल्या नंबर थिअरी संशोधनात हा डेल्टा आणि त्याच्या भाऊबंदांचं अनन्यसाधारण स्थान आहे. आता रामानुजनला ही उलथापालथ कोणी करायला सांगितली?! पण इथे तो विचक्षण स्वभाव त्याच्या गौरवशाली राजस स्वरूपात दिसून येतो. इथे साधारणच काय पण मोठे गणितज्ञसुद्धा नतमस्तक होतात.

ह्या डेल्टाचे प्रत्येक q ह्या मूळ संख्येसाठी सहगुणक असतात a(q). ह्याही नैसर्गिक संख्याच असतात. a(q) चा आकार साधारण (२q^6) म्हणजे साधारण qच्या ६ व्या घातापेक्षा जास्त नसतो, असं रामानुजनला सहज दिसलं. ह्याचं कारणही देता येतं. पण इतक्यावर थांबेल तर तो रामानुजन कसला! त्याने एक पाऊल पुढे टाकून 'रामानुजनचा तर्क' केला, की a(q) चा आकार (२q^6) पेक्षाच काय, पण (२q^(५.५)) पेक्षा कमी असला पाहिजे. हा तर्क आला, आणि सगळे संभ्रमात पडले. १२/२ ऐवजी ११/२ इतकाच हा फरक, पण तो आला कुठून?! आणि रामानुजनला कसा दिसला?! आश्चर्यच आहे. हा तर्क बरोबर आहे, हे सिद्ध केलं ते पिअरे डेलिननं १९७० च्या दशकात, म्हणजे ५० वर्षांनी. हे सिद्ध केल्याबद्दल डेलिनला गणितातील सर्वात मानाच्या पुरस्काराने अर्थात 'फिल्ड्स मेडल'ने गौरवलं गेलं. ह्या सिद्धतेमुळे नंबर थिअरी आणि अल्जिब्राईक जॉमेट्री ह्या महत्त्वाच्या शाखांत मोठी प्रगती झाली. रामानुजनच्या पाऊलखुणा ह्या अश्या दशकानुदशके आणि आता शतकानुशतके नवीन गणितज्ञांना मार्ग दाखवत गणितातल्या वाटांवर उमटल्या आहेत.

ह्याचबरोबर रामानुजनने त्याच्या शेवटच्या वर्षांत मॉक मॉड्युलर फॉर्म्स, मॉक थीटा फंक्शन्स अश्या अनेक महत्त्वाच्या संकल्पना शोधून काढल्या. अगदी अलीकडे त्यांचा संबंध अवचितपणे कृष्णविवरांशी आहे असे दिसून आले आहे. त्यामुळे पुढच्या शतकात ह्या कल्पना आणि त्यांचे सुंदर गुणधर्म अधिकच उठून दिसतील, ह्याविषयी माझ्या मनात कुठलीच शंका नाही. रामानुजन ग्राफ्स ही अशीच एक अभिनव कल्पना सध्या संगणकशास्त्रात अतिशय महत्त्वाची ठरली आहे. त्यामुळे गणितच काय पण भौतिकशास्त्र आणि संगणकासारख्या विषयांत रामानुजनशी 'आज अंतर्यामी भेटे' अशी गाठ पडत राहते.

रामानुजन नवनिर्मिती, सौंदर्यदृष्टी, विचक्षण बुद्धी, कल्पकता, मेधा, प्रज्ञा अश्या अनेक पातळ्यांवर कितीतरी सरस होता. आपलं एका अर्थी भाग्य की तो भारतीय होता. भारतीय गणिताची सुरवात एका अर्थी त्याच्यापासून झाली. कुठलीही पदवी नसताना हा भारतीय माणूस लंडनच्या रॉयल सोसायटीमध्ये फेलो झाला. भारतामधूनही असे गणिती येऊ शकतात, असा विश्वास आधुनिक जगाला वाटू लागला. परंतु आजच्या भारतात फक्त रामानुजनचं नाव घ्यायचं, परंतु त्याच्याविषयी, त्याच्या गणिताविषयी काहीच माहिती नाही, अशी प्रवृत्ती आहे. नाव रामानुजनसारख्या नवनवोन्मेषशालिनी प्रतिभेचं घेऊन मुलांना अतिशय साध्या आणि कुठल्याही नावीन्यपूर्ण नसलेल्या बळंच वैदिक म्हणवल्या जाणार्‍या गणितासारख्या सोप्या क्लृप्त्या शिकवण्यात वेळ घालवायचा, ही वृत्ती जोपासता कामा नये. भारताकडे आपला असा मोठा ठेवा आहे हे खरंच, पण तो नक्की कुठला, हे आपलं आपल्यालाच कळायला हवं. हा झरा असाच वाहता ठेवायला हवा. रामानुजन जाऊन २०२० मध्ये १०० वर्षं पूर्ण होतील. त्याला हीच खरी आदरांजली असेल.

(हा लेख प्रथम माहेर दिवाळी अंक २०१९ येथे प्रसिद्ध झाला. तो इथे पुनर्प्रकाशित करण्यासाठी परवानगी दिल्याबद्दल माहेरच्या संपादिका सुजाता देशमुख यांचा मी ऋणी आहे.)