गट्टी गणिताशी, मोदक दुप्पट खाशी

हिमालयाच्या पर्वतशिखरांवर सोनेरी धुकं चमकत होतं. कैलास आणि गुर्लमांधात्याची शिखरं मावळतीकडे झुकणार्‍या उन्हात न्हाऊन निघाली होती. मात्र अश्या उन्हात शांत आरामाऐवजी भगवान शंकराच्या घरी मात्र लगबगीचं वातावरण होतं. श्रीगणेश लवकरच त्यांच्या वार्षिक वारीला निघणार होते ना! सामानाची बांधाबांध किती 'झाली' म्हटलं, तरी शेवटपर्यंत काही ना काहीतरी असतंच. देवी पार्वती आपल्या बाळाला नेहमीप्रमाणे सूचना देत होती. "मोदक जास्त खाऊ नकोस हो!" "पावसात जास्त भिजू नकोस!" "मूषकाची काळजी घे." वगैरे. भगवान शंकरही कौतुकाने आपल्या मुलाच्या सोहळ्याची तयारी बघत होते. श्रीकार्तिकेय आणि मयूर मात्र इंद्रधनुष्याच्या पार्श्वभूमीवर नर्तनासाठी गेले होते. मूषकाची इकडेतिकडे तुरूतुरू पळापळ चालू होती.

हळूहळू सारं जरा थंडावलं. आई-बाबा जरा त्यांचं काम बघायला लागले, आणि श्रीगणेश आणि मूषक थोडा वेळ दम खायला म्हणून शांत देवासारखे म्हणतात तसे उदाहरणार्थ बसले. आईने लाडाने रांधलेल्या मोदकांचा फराळ होताच!

"व्वा! काय सुंदर जमले आहेत मोदक रे मूषका!" गणपती समाधानाने उद्गारला.

"हो देवा! असं वाटतंय की संपूच नयेत! एकामागोमाग एक खातच रहावेत." मूषक भरल्या तोंडाने आणि भरल्या मनाने म्हणाला.

"खरंच आईच्या हातच्या मोदकांची चव काही वेगळीच. पण माझे भक्तही किती किती छान छान प्रसाद आणतात माझ्यापुढे! मस्त मजा येते."

"हो देवा, माझीही चैन होते. ह्या वर्षी किंवा गेल्या वर्षी म्हणा, किती संकटं आली तरी भक्तगण तुझ्या सरबराईमध्ये कधीही काहीही कमी पडू देत नाहीत. तरी देवा, असेही काही लोक असतील, ज्यांना तुझं अजून खूप करायची इच्छा असेल. पण परिस्थितीमुळे ते होऊ शकत नसेल." मूषक थोडासा खिन्न होत म्हणाला.

"खरं आहे मूषका तुझं. कुठल्याही भक्ताने माझ्यापुढे आणलेला कोणताही प्रसाद माझ्यासाठी प्रेमाचा आणि गोडच असतो. एकविसशे मोदक असतील काय किंवा एकवीस साखरफुटाणे असतील तरी काय! भक्तीचं आणि भावाचं मोल माझ्यासाठी आहे. माझ्या भक्तांनाही मी हेच सांगतो. माझ्यापुढचा प्रसाद दिसायला कमी झाला, तरी माझे भक्त एकमेकांना मदत करत असतील, सहानुभूती आणि सहवेदनेने एकमेकांसाठी धावून जात असतील, सुखाने एकत्र नांदत असतील, तर तो माझ्यासाठी प्रसादच नाही का?" गणेश गंभीर होऊन सांगत होता.

"खरं आहे. शेवटी एकमेकांना मदत करणे, गुण्यागोविंदाने सर्वांनी नांदणे हेच महत्त्वाचं. पण तरी, काहीतरी चमत्कार त्यांच्याकडे असायला हवा होता. एका मोदकाचे दोन मोदक करू शकायचा, नाहीतर छोट्याश्या मोदकाचा मोठ्ठा मोदक व्हायचा चमत्कार!" मूषकमामाच्या कल्पनेच्या भरार्‍या उंच निघायला लागल्या.

"अशी काही जादू नसते, हे तर तुला माहितीच आहे. पण गंमत म्हणजे माणसांच्या भौतिक जगात असं काही होत नसलं, तरी गणिताच्या जगात तू म्हणतोस ते होतं बरं का! गंमतच आहे ती."

"म्हणजे .. नक्की काय होतं?! मला काही नीट कळलं नाही देवा."

"अरे तू म्हणतोस तेच. म्हणजे एका आकारमानाचा लाडूसारखा गोल असेल, तर त्यापासून त्याच आकारमानाचे दोन गोल निर्माण करता येतात. नाहीतर मटाराच्या दाण्याएवढा गोल असेल, तर तो सूर्याएवढा मोठासुद्धा करता येतो!" गणेश उत्साहाने सांगायला लागला.

"पण हे सगळं गणिताच्या जगात आहे ना? मग त्यात काय मोठंसं. तिथले आकार तर कसेही खेचता, ताणता येतात. ते अनंतप्रकारे लवचिक असतात. मग काय सरळ ताणायचं त्या गोलांना आणि कितीही मोठं करायचं."

"अरे तसं नाही. ते तर होऊच शकतं. त्यात काही मजा नाही. पण इथे मजा अशी आहे, की त्या सुरवातीच्या गोलाचं अश्या भागांमध्ये विभाजन करता येतं, की त्या प्रत्येक भागाला फक्त विशिष्ट प्रकारे गोल फिरवलं, आणि परत विशिष्ट प्रकारे जोडलं, की दोन गोलांमध्ये रूपांतर होतं!"

"छे:! असं कसं होऊ शकेल देवा? नुसतं गोल फिरवण्याने आकारमान बदलत नाही ना? मग आकारमान दुप्पट कसं होईल?" मूषकराजे गोंधळलेच जरा.

"अगदी बरोबर बोललास. जर आधीच्या भागाला आकारमान असेल, तर ते गोल फिरवण्याने बदलत नाही, हे अगदी बरोबर. माणूस स्वतःभोवती 'घालीन लोटांगण वंदीन चरण" म्हणत गरागरा फिरल्याने त्याचं आकारमान बदलत नाही. खूप केलं तर ढेरी जरा कमी होऊ शकते पण त्याची कारणं वेगळी आहेत. पण आधीच्या भागाला आकारमानच नसेल तर?" गणेशाच्या डोळ्यांत मिश्कील हसू होतं.

"म्हणजे? तुला असं म्हणायचंय की आकारमानच नसलेले संच असतात?!" मूषक बुचकळ्यातच पडला होता.

"हो. आपण जे नेहमी आकार बघतो, चौरस, आयत, वगैरे, त्या सर्वांना आकारमान असतं. पण गणितज्ञांची हीच गंमत आहे. ते सर्व शक्यतांचा विचार करतात आणि त्यांची प्रतिभा कधीकधी अशी थक्क करणारी झेप घेते, की मलासुद्धा मजा वाटते. आकारमान असलेल्या गोलाचं अश्या भागांमध्ये विभाजन करायचं, की ज्यांना आकारमानच नसतं, आणि त्यांना फक्त गोल फिरवून पुन्हा जोडलं, की दुप्पट आकारमान तयार होतं! दुप्पटच काय, कितीही पट आकारमान ह्याप्रकारे करता येऊ शकतं!"

"पण हे म्हणजे होतं कसं देवा? जरा अजून सांग ना!"

"अरे ही सगळी गंमत आहे ती अनंताची. एका गोलामध्ये अनंत बिंदू असतात हे आपल्याला माहितीच आहे. दोन गोलांमध्येही तितकेच आणि तेवढेच अनंत बिंदू असतात! माणसाला वाटू शकेल, की ते दुप्पट असतील, पण हे पटींचं गणित अनंताला तसंच्या तसं लागू होत नाही. एक अनंत हा त्याच्या स्वतःच्याच छोट्या भागाएवढाच असू शकतो!"

"हो, हे तू मला सांगितलं आहेस आधी. छोट्याश्या सीमित रेषाखंडामध्ये आणि मोठ्ठ्या असीमित रेषेमध्ये एकाच संख्येचे बिंदू असतात की! कसलं जबरदस्त आहे हे. ते इथे कसं वापरलं जातं?"

"तुला सगळं सांगत नाही इथे, पण चित्र दाखवतो. गोलाच्या बिंदूंचं एका विशिष्ट पद्धतीने एखाद्या रांगोळीत रूपांतर होतं, असंच समज."

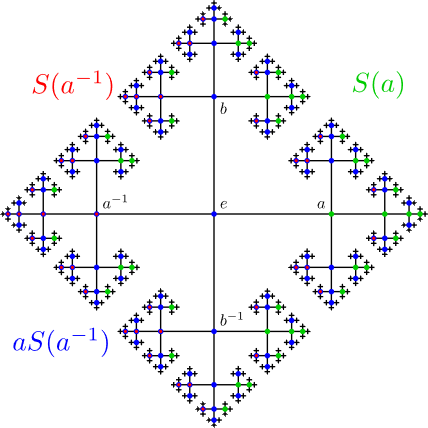
"व्वा! किती छान रांगोळी दिसतेय ही!"

"हो, पण लक्षात ठेव, इथे जरी ही रांगोळी अनंत दिसत नसली, तरी तिचे बिंदू अनंत आहेत बरं का! त्यामुळे तिचे भाग हे त्या रांगोळीएवढेच मोठे आहेत!"

"म्हणजे तू मला ते स्वसमानतेबद्दल सांगितलं होतंस, तसंच की हे! छोटा भाग आणि मोठी आकृती सारखीच दिसते."

"अगदी बरोबर! एकदा हे कळलं, की पुढची गंमत तुला दाखवतो बघ."

"व्वा! एकाचे दोन झाले! अनंताची कमाल! अद्भुत!" मूषक प्रसन्न होऊन उद्गारला.

"आहे की नाही मजा? स्टेफान बानाक आणि आल्फ्रेड तार्स्की ह्या दोन पोलिश गणितज्ञांनी ही कमाल शोधून काढली. जेउसेप विताली ह्या इटालियन गणितज्ञाच्या आणि फेलिक्स हाऊसडॉर्फ ह्या जर्मन गणितज्ञाच्या कामावर आधारित हा सिद्धांत त्यांनी १९२४ मध्ये प्रसिद्ध केला."

"जवळपास १०० वर्षे लोटली की म्हणजे ह्याला!"

"हो. त्या काळात गणितज्ञांच्या जगामध्ये ह्या सिद्धांताने चांगलीच खळबळ माजली होती." गणेश हसूनच म्हणाला.

"म्हणजे गणितज्ञांनाही ही जादू पटली नव्हती?"

"अनेकांना हे पटलं नव्हतं. पण सिद्धतेमध्ये काहीच तार्किक दोष नाही, हे सहज दिसत होतं. मग ज्यांना हे पटलं नाही, त्यांनी ह्यात वापरलेल्या गृहीतकांवर लक्ष केंद्रित केलं. बर्‍याच गृहीतकांवर शंका घेण्यासारखं काही नव्हतं. पण एक गृहीतक होतं ते म्हणजे 'निवडीचं गृहीतक'. अनंत संचांशी ह्याचा संबंध येतो. ह्या गृहीतकाची अंतःप्रेरणा माणसाला येणं जरा कठीण आहे. ह्या गृहीतकाच्या सत्यासत्यतेबाबत बरीच चर्चा झडली. आणि शेवटी 'निवडीच्या गृहीतकाला मानणारे' आणि 'निवडीच्या गृहीतकाला न मानणारे' असे गटच पडले. अशी गणितामध्ये एक प्रकारची क्रांतीच ह्या सिद्धांताने आणली. बरेचसे गणितज्ञ मात्र ह्या गृहीतकाला खरं मानूनच चालतात."

"खरं आहे. शेवटी प्रत्येकाला निवडीचं स्वातंत्र्य आहेच." उंदीरमामा हसून म्हणाले. गणेशही छानसं हसला.

"म्हणजे देवा, तू शून्यातून ह्या विश्वाची निर्मिती केलीस, तरी ही माणसंही काही कमी नाहीत तर! तीही अशी एकातून दुसर्‍याची निर्मिती करू शकतात की!"

"खरं आहे मूषका. मानवाच्या प्रतिभेला आणि इच्छाशक्तीला आभाळसुद्धा ठेंगणं पडेल. म्हणून तर मला प्रतिवर्षी जाऊन माझ्या भक्तांची विचारपूस करायला आवडते. त्यांचा उत्साह बघून मलाही नव्याने हुरूप येतो, हे तुला सांगायला नकोच!"

"चल तर मग, ह्यावर्षीही ते आपल्याला लवकर बोलावतायत. त्यांचा मान ठेवूया! तसंही इथले मोदक आपण संपवलेच आहेत!"

मोठ्याने हसत गणेश आणि मूषक दोघेही भक्तांकडे यायला आणि अजून मोदक खायला निघाले.

- भास्कराचार्य