आमच्या पूर्वजांना सग्गळं माहिती होतं का?

'गणितामध्ये भारतीयांचा वाटा नेहमीच सिंहाचा राहिला आहे' अश्यासारखी वाक्यं लहानपणापासून आपण ऐकत, वृत्तपत्रांमध्ये वाचत आलो आहोत. भारतीय लोक माहिती तंत्रज्ञान क्षेत्रात त्यामुळे पुढे आहेत, ही बाब आपल्या मनावर ठसली आहे म्हणा ना! शून्याचा शोध आपल्याकडे लागला, हेही आपण रास्त अभिमानाने सांगतो. त्यातून पूर्वीच्या काळात आपल्या पूर्वजांना सग्गळं सग्गळं ठाऊक असल्याचे व्हॉट्सअ‍ॅप फॉरवर्ड्स आपण नित्यनेमाने बघत असतोच. 'अमुक नावाच्या अक्षरांमध्ये ५ मिळवा, मग २ ने गुणा' इ. इ. तारेवरची वाटणारी कसरत करून शेवटी आपण इष्ट उत्तरापाशी आलो, म्हणजेच किती विचार करून आपल्या पूर्वजांनी हे साधलं असेल पहा, असं सांगणारे मेसेजेस असतात. आपल्यालाही ते करून मजा येते, यात वादच नाही. पण ह्यात गणित किती, आणि हातचलाखी किती, ते आपण कधीतरी बघायला हवं. 'वडिलांची किर्ती' सांगताना ती आपल्याला खरंच किती कळली आहे, हे आपण बघायला हवं. आपल्या माणसाचं कौतुक सांगताना थोडं अधिकच बोललं जातं हे खरंच. पण त्यातही तरतमभाव ठेवायला हवा. असं एक खरोखरच दैदीप्यमान आणि कौतुकास्पद उदाहरण म्हणजे ज्याला 'केरळ स्कूल ऑफ अ‍ॅस्ट्रॉनॉमी अ‍ॅण्ड मॅथमॅटिक्स' म्हणतात, ते इसवी सनाच्या चौदाव्या ते सोळाव्या शतकातले काही गणितज्ञ! खरंतर ह्यांच्याविषयी बोलताना मीच आपल्या माणसाचं जास्त कौतुक करण्याच्या मनस्थितीत आहे, कारण जरी नुसती ह्यांच्या 'नामाची साखर कागदी' लिहिली तरी खरंच 'मधुर गोडी' येते असं मला वाटत राहतं.

ब्रह्मगुप्त, आर्यभट, दोन्ही भास्कराचार्य ह्यांसारख्या गणितज्ञांची वैभवशाली परंपरा इसवी सनाच्या पहिल्या सहस्रकात आणि दुसर्‍या सहस्रकाच्या सुरवातीला भारताला लाभली होती. पण ह्यांतले फार गणितज्ञ किंवा खगोलशास्त्रज्ञ केरळातले होते, असं दिसत नाही. आर्यभट केरळातला होता, असा सिद्धांत काही लोकांनी मांडला आहे, परंतु त्याला फारसा आधार सापडलेला नाही. परंतु ह्या भूमीला विद्वानांची परंपरा होतीच. आदि शंकराचार्यांसारखे प्रज्ञावंत इथे होते. त्याचबरोबर केरळातून अनेक देशांमध्ये व्यापारमार्गे ज्ञान आणि संस्कृतीची देवाणघेवाण होत होती. पर्शियन आणि अरबी गणितज्ञांशी केरळच्या होणार्‍या संवादावर प्रकाश पाडण्याचं काम आता चालू झालं आहे. एकमेकांशी सुसंवाद साधल्याने ज्ञानाच्या कक्षा कश्या रुंदावतात, ह्याचं हे निश्चितच महत्त्वाचं उदाहरण आहे.

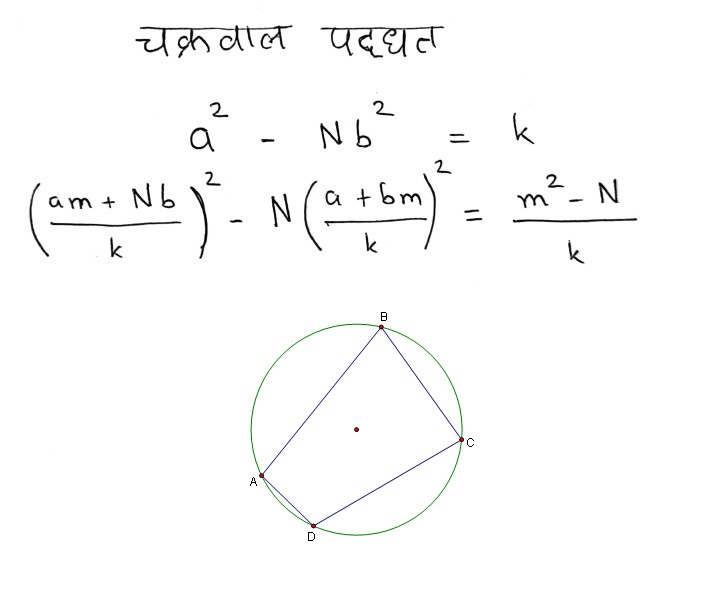
केरळ स्कूल ऑफ मॅथमॅटिक्समधला पहिला महत्त्वाचा गणितज्ञ म्हणता येईल तो म्हणजे नारायण पंडित. अदमासे इ.स. १३४०-१४०० हा ह्यांचा कालखंड असावा. 'गणितकौमुदी' आणि 'बीजगणित वातांश' हे दोन ग्रंथ त्यांनी रचले. दुसर्‍या भास्कराचार्यांनंतर भारतात गणिताचा झेंडा ह्या ग्रंथांनी पुढे नेला. माझ्या गेल्या वर्षीच्या रामानुजनवरील लेखात वर्गमूळ काढण्याची जी पद्धत साक्षेपात सांगितली होती, तिची मुहूर्तमेढ दुसर्‍या भास्कराचार्यांच्या आणि नारायण पंडितांच्या कामात आहे. तिचा वापर करून

ह्यांसारखी समीकरणे कशी सोडवावीत, ह्याचं विवरण नारायण पंडितांनी केलं. भास्कराचार्यांच्या कामाचं त्यांना सखोल ज्ञान होतं हे इतकं दिसतं, की भास्कराचार्यांच्या 'लीलावती' ह्या ग्रंथावरील एक प्रसिद्ध टीकाग्रंथही त्यांनीच लिहिला असावा, असा एक मतप्रवाह आहे. त्याचबरोबर चक्रीय चौकोनाच्या अनेक गुणधर्मांचा नारायण पंडितांनी अभ्यास केला होता, असंही अलीकडे दिसून आलं आहे. ब्रह्मगुप्ताच्या काळानंतर ह्या भूमितीकडे भारतीय गणितज्ञांचं थोडंसं दुर्लक्ष झालं असावं. नारायण पंडितांनी स्वयंप्रज्ञेने तिकडे पुन्हा लक्ष वेधून घेतलं.

नारायण पंडितांचा एक मोठा शिष्य म्हणजे परमेश्वर पंडित. इ. स. १३७० - १४६० हा ह्यांचा कालखंड असावा. माधव पंडित हे त्यांचे दुसरे गुरू असावेत. वास्तविक आपल्याला नारायण पंडितांच्या जन्मस्थळाविषयी किंवा कार्यस्थळाविषयी काहीच माहिती नाही. पण हे त्यांचे शिष्य केरळात अलत्तूर इथले होते, हे निश्चित माहिती आहे. त्यांचा कालखंडही योग्य प्रकारे सांगता येतो, कारण त्यांनी जवळपास ५५ वर्षं सूर्यग्रहणं आणि चंद्रग्रहणं बघून निरीक्षणं नोंदवली आहेत. त्यांनी आपल्या गुरूंचा वारसा पुढे नेत आधीच्या गणितज्ञांच्या कामावर टीकाग्रंथ लिहिले. त्याचबरोबर चक्रीय चौकोन ज्या वर्तुळात रेखला आहे, त्या वर्तुळाची त्रिज्या काढण्याचं सूत्र देणारे हे जगातले पहिले गणिती! युरोपियनांनी हे श्रेय ल्हुईलिये ह्या फ्रेंच गणितज्ञाला १७८२ मध्ये हे करण्याबद्दल दिलं आहे, पण त्याच्या ४०० वर्षं आधी हे सूत्र परमेश्वर पंडितांनी दिलेलं आहे. त्यांची अजून एक लक्षणीय कामगिरी म्हणजे आपण शाळाकॉलेजात शिकतो त्या 'मीन व्हॅल्यू थिअरम'ची एक अत्यंत सुरेख आवृत्ती त्यांनी 'लीलावती भाष्य' ह्या 'लीलावती'वरील टीकाग्रंथात लिहून ठेवलेली आहे! युरोपात ह्या विचारांचा प्रसार होण्यापूर्वी सुमारे ३०० वर्षं आधी हे आपल्याकडे व्हावं, हे यश नक्कीच दैदीप्यमान आहे. त्यांच्या ह्या कामावर माधव पंडितांचा प्रभाव निश्चित दिसून येतो.

वर ज्यांचा सातत्याने उल्लेख आलेला आहे, त्या माधव पंडितांकडे आपण आता यायलाच हवं. केरळ स्कूलच्या पंडितांचा सन्मान करून त्यांना आपण घरी पंगतीच्या जेवणाला पंचपक्वान्नं खायला बोलवलं, तर त्यातलं मानाचं पान माधव पंडितांकडे जाईल ह्याबद्दल माझ्या मनात तीळमात्र संशय नाही! संगमग्राम नावाच्या गावी इ.स. १३५० मध्ये ते जन्मले. आजच्या कोची शहराजवळ अलूर येथे हा भाग आहे. दुर्दैवाने माधव पंडितांनी स्वतः लिहिलेले कोणतेही ग्रंथ आता उपलब्ध असावेत असं दिसत नाही, पण त्यांच्या वंशजांनी त्यांना योग्य तो आदर देऊन त्यांनी शोधलेल्या सिद्धांत आणि सूत्रांबद्दल स्पष्ट लिहून ठेवलेलं आहे आणि त्यांचा यथोचित सन्मान केलेला आहे. त्यामुळे आपल्याला ह्या असामान्य गणितज्ञाची चमक ठायीठायी दिसून येते, आणि आकाशातच वीज चमकून लुप्त होऊन जमिनीवर पडली नसल्याने तिचा आवाजही झाला नाही, तरी त्या सौंदर्याने आपले डोळे दीपून आपण नतमस्तक व्हावं, तसं इथेही व्हायला होतं.

टेलर सिरीज, मॅक्लॉरिन सिरीज ही नावं आपण कॉलेजात ऐकली असतील कदाचित. षड्रिपूंसारखी त्यांच्याशी झुंजही घेतली असेल. ह्या सिरीजची मुहूर्तमेढ त्यांच्या युरोपात प्रकट होण्याआधी रोवली ती माधव पंडितांनी! गणिताचे इतिहासकार राजगोपाल आणि रंगाचारी ह्यांनी म्हटल्याप्रमाणे 'पुरातन गणिताच्या finite पद्धतींमधून त्यांचं limit घेण्याची निर्णायक झेप' जगाच्या पाठीवर पहिल्यांदा घेतली ती माधव पंडितांनी. हीच प्रक्रिया आपण कॅलक्युलसमध्ये पाहतो. आधुनिक गणितात ह्याचंच नाव मॅथमॅटिकल अ‍ॅनालिसिस आहे. ह्या प्रक्रियांचा पहिला ठाव माधव पंडितांनी घेतला. त्रिकोणमितीमध्ये भारतीय गणितज्ञांचं कौशल्या वादातीत होतंच. Sin x, Cos x, Tan x ह्यांची टेलर सिरीज १४०० सालाच्या आसपास माधव पंडितांनी शोधून काढली. त्यांनी ह्याची रीतसर पद्धतच दिली आहे. ती पुढीलप्रमाणे - (संस्कृतमधून साधारण भाषांतर करून)

(१) कंसाला कंसाच्या वर्गाने गुणावे, आणि हीच प्रक्रिया कितीही वेळा करावी, आणि येणारी उत्तरं लिहावीत.

जर s कंसाची लांबी असेल, तर ह्या पहिल्या पायरीतून

ही उत्तरं येतात.

(२) वरच्या प्रत्येक उत्तराला क्रमाने येणार्‍या सम संख्यांचा वर्ग करून त्यात तीच संख्या मिळवून जी संख्या येईल, तिला त्रिज्येने गुणून येणार्‍या संख्येने भागावे.

हे कितीही समजायला 'अबब!' असं वाटलं, तरी आहे बैजवार. त्रिज्या जर r असेल, तर ह्या पायरीतून आपल्याला

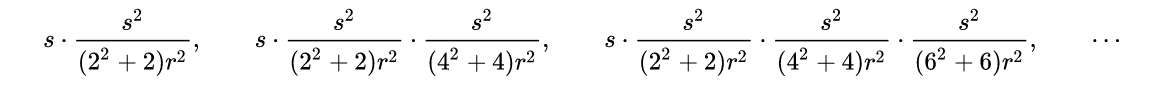
ह्या संख्या मिळतात.

आता शेवटची पायरी.
(३) कंस आणि वरून मिळालेली उत्तरं एकापुढे एक ठेवा, आणि प्रत्येक आधीच्या उत्तरामधून वजा करा, म्हणजे तुम्हाला त्या कंसाच्या जिवेची लांबी मिळेल!

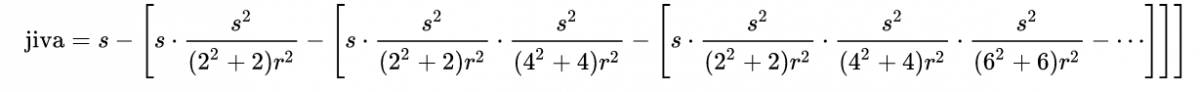
जर x हा कंसाने केंद्रबिंदूशी केलेला कोन असेल, तर s = r.x असते, आणि जिवा = r. sin x असते. त्यामुळे हेच समीकरण सरळ सोडवून

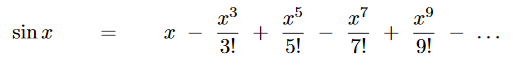
असे दिसते. हीच सुप्रसिद्ध Sin x ची टेलर-मॅकलॉरिन सिरीज! (जिला खरं तर माधव पंडित सिरीज म्हणायला हवे.)

ह्यात ... ही जी प्रक्रिया आहे, ती अनंत (infinite) वेळा वजाबाकी करण्याची क्रिया दर्शवते. गणितज्ञांना ही क्रिया करणे म्हणजे नक्की काय, हे जाणून घ्यायला हजारो वर्षे जावी लागली. गणिती सौंदर्यभाव (aesthetic sense) म्हणतात तो हाच! एक गणितज्ञ म्हणून मला ही अशी बुद्धीची झेप बघितल्यावर फार गदगदून जायला होतं. विस्तारभयास्तव मी येथे ह्या सगळ्याची अजून फोड करून सांगू शकत नाही, ह्याची खंत वाटते. पण ही व्यक्ती आपल्या मातीत होऊन गेली, ह्याचा आपल्याला ज्ञाना-तुक्याबद्दल जसा आनंद वाटतो, तसाच आनंद वाटायला हवा, एवढेच म्हणतो.

माधव पंडितांनी अशी अनेक अनंताची खूणगाठ बांधणारी समीकरणे लिहिली. Sin x सारखीच Cos x आणि Tan x चीदेखील सिरीज त्यांनी लिहिली. त्याचबरोबर arcsin, arccos, arctan ह्यांच्याही सिरीज त्यांनी लिहून ठेवल्या. arctan x च्या सिरीजमध्ये x = 1 टाकल्यास

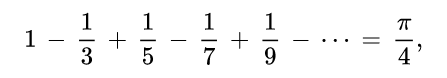
हे 'पाय'साठीचे नितांतसुंदर सूत्र त्यांनी दिलं. १६६८ साली, म्हणजे जवळपास ३०० वर्षांनंतर हे सूत्र ग्रेगरीने युरोपात शोधले, आणि त्यानंतर लायब्निझने ते १६७४मध्ये पुन्हा शोधले. ह्या सिरीजचा वापर करून माधव पंडितांनी 'π'ची किंमत ११ दशांशस्थळांपर्यंत अचूक निश्चित केली.

माधव पंडितांचं योगदान फार मोठं आणि वादातीत आहे. इथे ते पूर्ण सांगताही येणार नाही. गेल्या काही वर्षांतच त्यांच्या कामाविषयी जागरूकता वाढली आहे. ती अजूनही वाढायची आवश्यकता आहेच. भारतीय गणितज्ञांची अशी मोठमोठी कामं आपल्याच अज्ञानामुळे दुर्लक्षित राहून जातात, असं मात्र व्हायला नको. त्यासाठी आपल्या इतिहासाकडे डोळसपणे बघण्याची गरज आहे.

केरळ स्कूल ऑफ मॅथमॅटिक्समधलं पुढचं महत्त्वाचं नाव म्हणजे नीळकंठ सोमयाजि. १४४४-१५४४ अशी त्यांनी वयाची १०० वर्षं पूर्ण केली. कुंडग्राम असं त्यांच्या गावाचं नाव. हे आजच्या काळात तिरूर गावात येतं. माधव पंडितांचं उपरोल्लेखित संशोधन, आणि स्वतःचंही भरपूर महत्त्वाचं काम त्यांनी 'तंत्रसंग्रह' ह्या फार फार महत्त्वाच्या ग्रंथात लिहून ठेवलं आहे. हे काम इतकं महत्त्वाचं आहे, की माधव पंडितांखालोखाल नीळकंठ पंडितांचाच उल्लेख व्हायला हवा. त्यांच्या कामाचं वैशिष्ट्य म्हणजे त्यांनी खगोलशास्त्रातही फार पायाभूत काम केलं. टायको ब्राहे आणि योहान केपलर ह्या खगोलशास्त्रज्ञांनी पृथ्वीकेंद्रित सिद्धांत दूर सारण्यात जो महत्त्वाचा हातभार लावला, ते काम त्यांच्या १०० वर्षं आधीच तंत्रसंग्रहात बर्‍याच अंशी दिसून येतं. बुध आणि शुक्र ह्या ग्रहांसाठी केप्लरची आकडेमोड आणि नीळकंठ पंडितांची आकडेमोड अगदी सारखी आहे. पण बाह्य ग्रहांसाठी केप्लरची समीकरणं आणि सिद्धांत जास्त योग्य ठरले. पण तरीही नीळकंठ पंडितांचा कालखंड आणि उपलब्ध सामग्री पाहता त्यांची निरीक्षणं आणि निष्कर्ष सोन्याच्या कसाचेच आहेत, ह्यात शंकाच नाही. ग्रहांच्या कक्षा आणि त्यांच्या अक्षांबद्दलची त्यांची अनुमाने अचूक होती. एक लंबवर्तुळाकृती कक्षेचा सिद्धांत सोडल्यास केप्लरचे इतर सर्व सिद्धांत तंत्रसंग्रहातून सिद्ध होतात, असे २००० साली शिमल्यात झालेल्या एका परिषदेत दाखवून दिले गेले. ही परिषद तंत्रसंग्रहास ५०० वर्षे पूर्ण झाली, ह्यानिमित्ताने भरवण्यात आली होती.

ह्या मालिकेतलं पुढचं महत्त्वाचं एक नाव म्हणजे ज्येष्ठदेव. इ. स. १५००-१५७५ हा ह्यांचा काळ होता. 'युक्तिभाषा' ह्या मल्याळममध्ये लिहिलेल्या ग्रंथात त्यांनी माधव पंडित ह्यांचे सिद्धांत, प्रमेये, आणि सूत्रे, तसेच तंत्रसंग्रहातील अनेक सिद्धांत आणि सूत्रे आणि त्यावर त्यांचे काम दिले आहे. ह्या ग्रंथाचे महत्त्वाचे वैशिष्ट्य म्हणजे ह्यात अनेक सिद्धता आहेत. इतर भारतीय ग्रंथांमध्ये सिद्धता देण्याची पद्धत नव्हती. त्यामुळे हा ग्रंथ भारतीय परंपरेच्या दृष्टीने फार महत्त्वाचा ठरतो.

ह्याशिवाय शंकर वारियावर, गणेश दैवज्ञ असे अनेक गणितज्ञ ह्या तार्‍यांच्या माळेत गुंफले गेले आहेत. सार्‍यांचीच कामगिरी इथे देता येत नसली, तरी एक समर्थ आणि निर्मितीक्षम परंपरा केरळला आणि भारताला ह्या जवळपास २००-३०० वर्षांच्या कालखंडात लाभली होती, ह्यात शंकाच नाही. भारतीय गणितज्ञांनी पुरातन काळातील आर्यभट, भास्कराचार्य, ब्रह्मगुप्त इ. गणितज्ञांचा वारसा ह्या काळात अधिकच पुढे नेऊन आधुनिक गणितापर्यंत आणला. माधव पंडित, नीळकंठ सोमयाजि, ह्यांचे काम रामानुजनसारखेच महत्त्वाचे आहे, आणि ते भारतीयांपर्यंत पोहोचणे गरजेचे आहे.

सरतेशेवटी आपण परत येतो, ते आपल्या मूळ प्रश्नांकडे. आपल्या पूर्वजांना अनेक गोष्टींचं ज्ञान होतं, हे आपण उदाहरणासकट पाहिलं आहे. इतकं, की अगदी 'न्यूटन-लायब्निझ' ह्यांच्या आधी कॅलक्युलस (कलनशास्त्र) आपल्याकडे माहिती होतं, असं म्हणण्याचा मोह होतो. परंतु माधव पंडितांबद्दल आणि ह्या इतर गणितज्ञांबद्दल इतकं प्रेम मनात असूनही मी असं सरसकट म्हणणार नाही. भारतीय गणितज्ञांनी अनंत सिरीज पहिल्यांदा शोधल्या, हे अगदी खरं. परंतु त्यांनी त्यांची विशिष्ट उदाहरणं Sin x वगैरेसाठी शोधली, तरी त्यांनी कुठल्याही f(x) साठी असा प्रयत्न केल्याचं दिसत नाही. त्याचबरोबर न्यूटन आणि लायब्निझ दोघांचीही कॅलक्युलसकडे जाण्याची विचारपद्धती इतिहासाला माहिती आहे. त्या दोघांनीही 'डिफरन्शिएशन' आणि 'इंटिग्रेशन' ह्या संकल्पनांचा 'थिअरी' म्हणून केलेला विकास केरळ स्कूळच्या कामात दिसत नाही. केरळ स्कूलच्या कामात ते अध्याहृत दिसतात हे खरेच, आणि त्याबद्दलही त्यांचे कौतुक करावे तितके थोडे आहे. पण कॅलक्युलसचा 'शास्त्र' म्हणून विकास करण्यातले न्यूटन-लायब्निझ आणि इतर युरोपिय गणितींचे योगदान वादातीत आहे, हे नक्की. त्यामुळे आमच्या पूर्वजांना सग्गळं माहिती आहे, असा ग्रह ह्या लेखातून करून घेणे बरोबर होणार नाही, पण त्यांच्या कामगिरीकडे डोळसपणे आणि रास्त आनंदाने पाहणे मात्र अभिप्रेत आहे.

एका मुद्द्यावर मात्र संशोधन होणे आवश्यक आहे, आणि होतही आहे, हे नक्की. केरळचा व्यापारमार्गे अनेक अरब आणि पर्शियन राज्यांशी संबंध आला. आणि ह्याच गणितज्ञांचा युरोपशीही व्यवहार चालू होता. त्याचबरोबर अनेक 'जेझुईट' मिशनरी केरळात कार्यरत होते. त्यामुळे काही कल्पना केरळमधून युरोपात गेल्या असण्याची नक्कीच शक्यता आहे. तशी काही कागदपत्रे मिळालेली नाहीत, पण तसा शोध आत्तापर्यंत फार कोणी घेतला नव्हता. तो आता इतिहास संशोधक घेत आहेत. न्यूटन-लायब्निझ नाही, तरी त्यांच्या आधी फर्मा, रोबरव्हाल अश्या काही गणितज्ञांना काही कल्पना केरळमधून मिळाल्या असल्याची शक्यता आहे. ह्याचा मागोवा घेतल्यास चित्र अजून स्पष्ट होईल. त्याचबरोबर उपरोल्लेखित कामांमध्ये अरब आणि पर्शियन गणितज्ञांच्या कल्पनाही कुठेकुठे दिसून येतात. त्यामुळे ज्ञानाचा हा धांडोळा सर्व बाजूंनी घेतला गेला पाहिजे. आणि हे जाणून घ्यायला हवं, की फक्त आपल्याच पूर्वजांनी सगळं शोधून काढलं असेल, असा विचार करण्यापेक्षा मानवजातीचा ह्या सर्व कल्पनांमधून विकास होणं ही किती आश्चर्यकारक गोष्ट आहे. ह्या वाटचालीमधला काही वाटा हा केरळ स्कूल ऑफ मॅथमॅटिक्ससारखा आपल्या देशातून आला, ह्यावर फुका गर्वाभिमानी बनण्यापेक्षा आत्ता ह्या घडीला आपल्या देशामधून, मनामधून गणिताची भीती घालवून ज्ञानाचा उदय कसा होईल, ह्याचा विचार केला पाहिजे. माधव पंडित आणि केरळ स्कूलला तीच खरी मानवंदना असेल.

(हा लेख २०२०च्या 'माहेर' दिवाळी अंकात प्रसिद्ध झाला होता.)