जीवनात ही घडी अशीच राहू दे (स्व-साधर्म्य - भाग २)

मागच्या भागात (आकाश के उस पार भी आकाश है (स्व-साधर्म्य - भाग १)) आपण मँडेलब्रॉटने उपस्थित केलेला प्रश्न पहिला. त्या अनुषंगाने कोखचा वक्र आणि अपूर्णांक भूमिती याबद्दलही काही वाचले. या स्व-साधर्म्यामुळे अतिशय कमी क्षेत्रफळाच्या आत प्रचंड मोठ्या लांबीची रेष, रेष म्हणण्यापेक्षा वक्र, कसा काय सामावू शकतो ते पाहिले. सृष्टीमध्ये विलसत असलेले स्व-साधर्म्य मँडेलब्रॉटच्या ध्यानात आले आणि यातूनच प्रेरणा घेऊन त्याने आकृत्यांशी बरेच खेळ केले. अशा स्व-समान गुणधर्म असलेल्या कित्येक आकृत्यांना त्याने जन्म दिला आणि गणिताच्या सहाय्याने कलेशी देखिल दुवा जोडला.

त्याने स्व-साधर्म्य असलेल्या अनेक आकृत्यांना जन्म दिला. त्यांना मँडेलब्रॉटचा संच (Mandelbrot's set) असेही नाव आहे. त्या आकृत्यांना असलेले गणिती मूल्य उलेखनीय आहेच, पण एक नक्षीकाम या दृष्टीने कलाक्षेत्रातही त्यांना खूप महत्व आहे. आपण त्यापैकी काही खाली दिलेल्या आकृत्या पाहून तूर्तास त्यातल्या कलेचा आस्वाद घेऊ.

(स्व-साधर्म्य हा गुणधर्म असलेल्या वरील आकृत्यांमध्ये झूम इन करत गेल्यास आतमध्येही पुन्हा तीच आकृती दृष्टीस पडेल.)

मागच्या भागात आपण पाहिले की या गुणधर्मामुळे कोखच्या वक्राची लांबी अनंत असली तरी ती संपूर्णपणे एका छोट्याश्या वर्तुळाच्या आत वेटोळे घालून बसली आहे. आता हेच स्व-साधर्म्य ३ मितींमध्ये (3 dimensions) कसे पाहता येईल ते बघू. एक घन ठोकळा (cube) घ्या. त्याच्या सगळ्या बाजूंच्या मधून एक एक छोटा ठोकळा काढून टाका (खालची आकृती पाहिल्यास कल्पना येईल). आता मूळच्या ठोकळ्यापेक्षा नवीन अर्धवट पोकळ ठोकळ्याचे घनफळ (volume) कमी झाले आहे. पण त्याच वेळेला ठोकळ्याचा आतला थोडा भाग उघडा पडल्यामुळे त्याचे बाह्य क्षेत्रफळ (outer surface area) वाढले आहे. अर्थात ठोकळ्याबाहेर हवा आहे असे मानल्यास हवेच्या संपर्कात आता ठोकळ्याचा जास्त भाग आला आहे. त्याचप्रमाणे आता ठोकळ्याच्या उरलेल्या भागातूनही आणखी छोटे छोटे ठोकळे काढून टाका. आता त्याचे घनफळ आणखी कमी होऊन हवेच्या संपर्कातले क्षेत्रफळ आणखी वाढलेले असेल. त्याप्रमाणे उरलेल्या भागातून आणखी छोटे छोटे ठोकळे काढत न्या आणि ही कृती अनंत काळ केल्यास तो ठोकळा संपूर्णपणे पोखरला जाऊन त्याचे घनफळ जवळपास शून्य होईल परंतु त्याचे क्षेत्रफळ हे प्रचंड जास्त, अनंत होऊ शकेल. तो ठोकळा पोकळ पोकळ छिद्रे असलेल्या स्पंजप्रमाणे दिसू लागेल.

( मेंगरचा स्पंज)

आता मँडेलब्रॉट म्हणतो की ह्या आकृतीच्या मिती किती? दुरून पाहिल्यास हा घन दिसतो, त्या अर्थी तो त्रिमितीय (three dimensional) आहे. पण त्याचे घनफळ तर शून्य आहे, म्हणजे तो धड त्रीमितीय नाही. शून्य घनफळ आणि खूप मोठे क्षेत्रफळ म्हणजे त्याला द्विमितीय (2 dimensional) म्हणावे का? कारण द्विमिती मधल्या आकृत्यांना कितीही मोठे क्षेत्रफळ असले तरी त्यांचे घनफळ शून्य असते. पण ह्या आकृतीला पाहता द्विमितीय म्हणणेही चुकीचे ठरेल. म्हणजे याची मिती २ किंवा ३ नसून त्या मधील कुठली तरी आहे. ते किती हे कसे शोधावे याची पद्धत मँडेलब्रॉटने दिली आहे. सध्याच्या लेखमालेचा उद्देश प्रमेयांच्या फार खोलात जाणे हा नसल्यामुळे त्यात मी शिरत नाही. वरील आकृतीची मिती साधारणपणे २.७२६८ इतकी आहे एवढेच सध्या सांगून थांबतो. सांगायची गोष्ट, की १, २ किंवा ३ मितीने समजावता न येणाऱ्या ह्या आकृत्यांची मिती अपूर्णांक (fractional dimensions) आहे. त्यामुळे जन्मलेल्या ह्या नव्या प्रकारच्या भूमितीला अपूर्णांक भूमिती किंवा fractal geometry असे नाव आहे.

कुठे कुठे दिसते ही अपूर्णांक भूमिती? इकडे तिकडे कशाला पाहता! आपले शरीर हीच एक अपूर्णांक भूमिती आहे. आपल्या डोक्याच्या कवटीच्या आत सामावलेला आपला मेंदू. त्यात इतक्या घड्या घड्या आहेत कि ते उलगडायचा प्रयत्न केल्यास कितीतरी मोठा आकार होईल. आपले फुफ्फुस (lungs) हे असेच एक उत्तम उदाहरण. आपल्याला किती जास्त प्रमाणात प्राणवायू (oxygen) हवेतून शोषून घेता येईल हे आपल्या फुफ्फुसांच्या क्षेत्रफळावर अवलंबून असते. जितके क्षेत्रफळ अधिक तितका प्राणवायूचा पुरवठा अधिक. आपली फुफ्फुसे याकरिता अनेक नळ्या, फांद्या, दुभंगणाऱ्या छोट्या फांद्या अश्या आकारांनी बनलेली आहेत. यामुळे फुफ्फुसांचे क्षेत्रफळ इतके मोठे असते कि ते मोजल्यास एका टेनिस ग्राउंडच्या क्षेत्रफळाइतके भरेल! पण इतके मोठे क्षेत्रफळ असलेले आपले फुफ्फुस आपल्या छातीच्या पिंजर्याच्या आत एका ठराविक आकारात बसलेले आहे हे नवलच नव्हे काय?

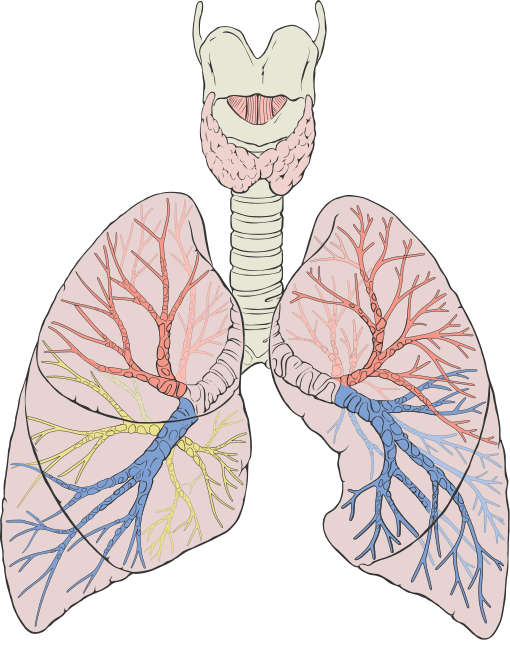
याच प्रकारे आपल्या रक्तवाहिन्या हेही एक उत्तम उदाहरण आहे. आपल्या संपूर्ण शरीरभर हे रक्तवाहिन्यांचे जाळे अश्या प्रकारे पसरले आहे कि शरीराच्या सर्व भागात रक्ताचा पुरवठा होऊ शकेल. आपल्या शरीरातले एकूण रक्त गोळा केल्यास ते संपूर्ण शरीराच्या घनफळाच्या १०% सुद्धा भरणार नाही. परंतु त्यांचे जंजाळ इतके आहे, की शरीराच्या कुठल्याही उतीपासून (tissue पासून) फक्त ४ पेशी एवढ्या अंतरावर जा, तुम्हाला एक तरी रक्तपेशी सापडेलच. या रक्तवाहिन्या म्हणजे कोखच्या वक्राप्रमाणे एका ठराविक आकारात सामावलेल्या प्रचंड लांबीच्या रेषा आहेत. त्यामुळे मँडेलब्रॉटने जे म्हटले आहे, की "तुम्ही रक्ताचा थेंबही न सांडू देता शरीराचे १ मिलीग्राम एवढेही मांस काढू शकत नाही" त्यात अतिशयोक्ती काहीच नसावी. (अश्याच अर्थाची एक बिरबलाची गोष्टही बहुश्रुत आहे.)

अश्याप्रकारे आपल्या शरीरात, बाहेर, आपल्या अवती-भोवती सगळीकडे घड्या, वळणे, फांद्या यांच्या रुपात आपल्याला हि अपूर्णांक भूमिती वसलेली दिसेल. या नव्या दृष्टीने सभोवार पाहू जाता संपूर्ण जीवनच या अपूर्णांक भूमितीने, घड्या-घड्यांनी व्यापलेले दिसेल, आणि मग 'जीवनात ही घडी अशीच राहू दे' हे गाणे ऐकताना त्याला एक नवीनच अर्थ प्राप्त होईल! खरच या शास्त्रज्ञांची दृष्टी मुळातच अशी असते का, कि सृष्टी स्वत:हून आपली गुपिते त्यांच्या समोर उघडी करते? कुणास ठाऊक! पण निदान त्यातला काही अंश आपल्याला बघायला मिळाला आणि सृष्टीकडे पाहण्याची वेगळी दृष्टी प्रयत्नांनी मिळाली तरी खूप आहे!

- शंतनु

मूळ लेख माझ्या स्वतःच्या ब्लॉगवरून पुनःप्रकाशित. हा लेख इतरत्रही प्रकाशित.

Material licensed under a Creative Commons Attribution-NoDerivatives 4.0 International.

(सर्व चित्रे विकिपिडीयावरून साभार)
मूळ भाग १ व २ च्या संपादनास मदतीबद्दल व प्रोत्साहनाबद्दल रोहित व अमिता यांचे आभार.