आपल्याला असा कधी प्रश्न पडला आहे का, की माणूस नेहमी सगळ्या वस्तूंना ठराविक आकारच का देतो? आमची घरे चौकोनी असतात. आमची पुस्तके चौकोनी, संगणकसुद्धा एका विशिष्ट आकाराचा; सगळीकडे चौकोन, आयत, त्रिकोण, गोल हेच आकार. आम्ही एखादे वेळी त्रिकोण किंवा पिरेमिड बांधतो. पण पृथ्वीवर सगळीकडे जमीन उंच-सखल आहे, आम्ही ती सपाट करून टाकतो. खोल भागात भराव टाकतो, डोंगर फोडून काढतो. पण सृष्टी अशी कुठे आहे? कुठला डोंगर अगदी बरोबर त्रिकोणी अथवा शंकू आकाराचा असतो? ढगांना कधी विशिष्ट आकार असतो का? आपले हात, पाय, नाक, डोळे, सगळेच वेगळे आकार. हे आकार आपण भूमितीमध्ये शिकतच नाही. सगळ्या गोष्टींना आपण सोप्या आकृत्यांमध्ये पाहायला शिकतो. लहानपणी आपण माणसाचे चित्र काढताना डोके गोल काढतो. हात-पाय सरळ रेषांनी दाखवतो. किंबहुना भूमितीच्या ठराविक आकृत्यांचा मनावर पगडा बसल्यामुळे आपल्याला सृष्टीमधल्या खऱ्या आकृत्या चित्राच्या रूपात रेखाटणे अवघड जाते.


(आपण काढतो तसे बाळबोध चित्र)
तर ते असो. ह्याबाबत आणखी पुढे सविस्तर बोलूच; पण त्या आधी ऐका एक कहाणी. एक आट-पाट कंपनी होती. तिचे नाव IBM. तिथे मँडेलब्रॉट नावाचा एक हुशार शास्त्रज्ञ काम करीत होता. तसा तो हाडाचा गणितज्ञ, पण भूमितीसह अर्थशास्त्र, माहिती-सिद्धांत (information theory), वहन-यांत्रिकी (fluid mechanics) सारख्या अनेक क्षेत्रांमध्ये त्याने नाक खुपसले होते. तो नेहमी म्हणायचा - "Clouds are not spheres, mountains are not cones, lightening does not travel in a straight line". खरी भूमिती ही उंच-सखलपणा, खड्डे, वळणे, घड्या, गुंता अश्या गोष्टींनी भरलेली आहे. मँडेलब्रॉटचे म्हणणे होते की या सर्व वर-वर अनियमित वाटणाऱ्या गोष्टींना अर्थ आहे आणि यांमध्येच अनेक गोष्टींचे मर्म दडलेले आहे. उदाहरणार्थ समुद्रकिनाऱ्याच्या लांबीचे मर्म काय आहे? मँडेलब्रॉटने असा प्रश्न एका शोधनिबंधामध्ये विचारला कि "ब्रिटनचा समुद्रकिनारा किती लांबीचा आहे?" आणि या प्रश्नाने जणू काही विचारांना नवी दिशाच मिळाली. सांगतो कसे ते.
१९३० च्या दशकात ल्युईस रिचर्डसन या ब्रिटीश शास्त्रज्ञाला समुद्रकिनारे आणि दोन राष्ट्रांमधल्या सीमारेषा यांच्या बद्दल कुतूहल होते. त्याने स्पेन आणि पोर्तुगाल, बेल्जियम आणि नेदरलंडस् या देशांमधले एनसाय्क्लोपिडीया पाहिले आणि त्याच्या असे ध्यानात आले की सामायिक (common) सीमारेषा असल्या तरी दोन देशांच्या नोंदींमध्ये (सीमारेषांची लांबी) साधारण २० टक्क्यांचा फरक आहे. अनेकांना तो खोटा वाटला. काहीजण म्हणाले, 'असेल बुवा. हे काही माझे क्षेत्र नाही'; काहीजण म्हणाले, 'मी एनसाय्क्लोपिडीया बघून सांगतो.' मँडेलब्रॉटच्या वाचनात हा लेख आला. त्याचे काय म्हणणे होते, की कुठलीही भौगोलिक सीमा ही एका अर्थाने अनंत लांबीची असते. दुसऱ्या शब्दात सांगायचे तर तुम्ही मोजमापासाठी कोणती पट्टी वापरता त्यावर तुम्ही मोजलेली एकूण लांबी किती भरेल हे ठरते.
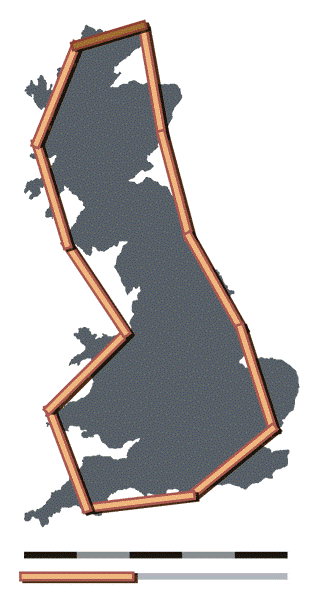
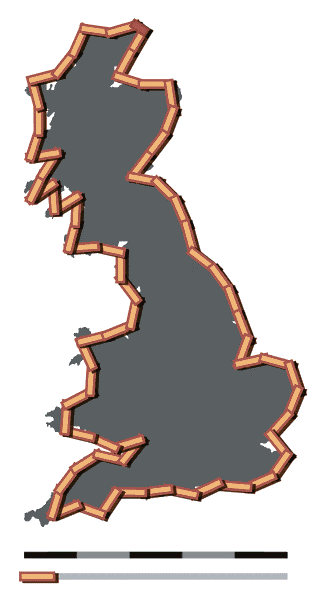
(ब्रिटनच्या समुद्रकिनाऱ्याची लांबी मोजायचा एक प्रयत्न (अ) एक २०० किलोमीटर लांबीची पट्टी वापरून आणि (आ) एक ५० किलोमीटर लांबीची पट्टी वापरून)
आता एक प्रात्यक्षिकच पाहू. वर दिलेल्या आकृतीमध्ये डावीकडे ती लांबी मोजण्यासाठी २०० कि.मी. लांबीची पट्टी वापरली आहे, तर उजवीकडे ५० कि.मी. लांबीची पट्टी. डावीकडच्या पट्टीने मोजल्यास एकूण लांबी २४०० किलोमीटर भरते तर उजवीकडच्या पट्टीने मोजल्यास ती ३४०० किलोमीटर भरते. इथे आपल्या डोळ्यांना सहज लक्षात येण्यासारखी गोष्ट आहे कि २०० कि.मी. ची पट्टी बरीच वळणे, ओबड-धोबडपणा पाहू शकत नाही. आता आपण पट्टी आणखी छोटी करत गेलो, तर आणखीन छोटी छोटी नागमोडी वळणे आपण मोजू शकू. पट्टी जितकी छोटी तितके जास्त बारकावे आपल्याला कळतील आणि एकूण लांबीचा आकडा तितकाच जास्त फुगत जाईल. दूर यानातून आपल्याला जितकी लांबी मोजता येईल, त्यापेक्षा जास्त लांबी समुद्र-किनाऱ्यावर चालत फिरणारा माणूस मोजू शकेल. त्याही पेक्षा जास्त लांबी एकेक खडा पार करत जाणारी गोगलगाय मोजू शकेल (अर्थात तिला तितका संयम हवा).
आता काही वेळापुरते आपण भूमितीकडे वळू आणि नंतर पुन्हा या भौगोलिक प्रश्नाकडे येऊ. त्याचे काय झाले, की १९व्या शतकाच्या सुरुवातीला 'कोख' नावाचा एक स्वीडिश गणितज्ञ होऊन गेला. त्याने आकृत्यांबाबत अनेक खेळ केले. त्याच्या नावाने 'कोखचा वक्र’ (Koch's curve) म्हणून एक आकृती ओळखली जाते. अत्यंत सोपी, पण त्यात एक मर्म दडले आहे अशी ही आकृती. ती कशी आहे ते आता आपण पाहू.
सुरुवातीला एक त्रिकोण घ्या. (त्याच्या प्रत्येक बाजूची लांबी '३' इतकी आहे असे आपण समजू. त्या ३ ला परिमाण काय हवे ते! म्हणजे त्रिकोणाची परिमिती ९ इतकी झाली.) त्याची प्रत्येक बाजू तिनात भागा. आता प्रत्येक मधल्या छोट्या भागावर आणखी एक छोटा त्रिकोण बांधा (ज्याची प्रत्येक बाजू अर्थात १ इतकी असेल). तयार झालेल्या आकृतीची बाह्य परिमिती १२ इतकी होईल. अशातऱ्हेने त्या छोट्या त्रिकोणांनाही भागून त्यांच्यावर आणखी छोटे छोटे त्रिकोण बांधत राहिल्यास पुढची बाह्य परिमिती १६ इतकी होईल. (बाह्य परिमिती म्हणजे काय? - खाली दिलेल्या आकृत्यांमध्ये केवळ काळ्या रंगाच्या रेषा पहा).
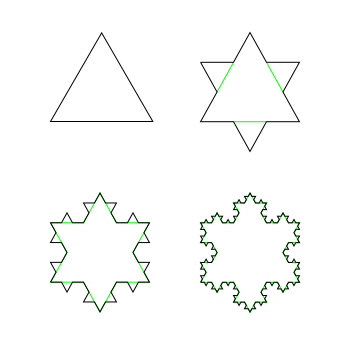
(त्रिकोणापासून सुरुवात करून त्यावर आणखीन छोटे छोटे असे त्रिकोण रचत गेल्यास मिळणारी आकृती)
म्हणजे थोडक्यात, आपण जसे आणखी छोटे छोटे त्रिकोण बांधत जाऊ, तशी नवीन आकृतीची परिमिती आधीच्या आकृतीच्या ४/३ पट होते. आता असे छोटे छोटे त्रिकोण अनंत काळ बांधत बसल्यास एकूण परिमिती ४/३ च्या पटीत वाढत वाढत जाऊन अनंत होईल. याच आकृतीचे नाव ‘कोखचा वक्र’. गंमत म्हणजे पहिल्या त्रिकोणाच्या तीनही बिंदूंमधून जाणारे एक वर्तुळ काढले तर असे लक्षात येईल की आपण पुढे कितीही त्रिकोण-त्रिकोण वाढवत बसलो तरी संपूर्ण आकृती त्या वर्तुळाच्या आतच राहते आहे. म्हणजे ही अनंत लांबीची रेषा एका छोट्याच्या वर्तुळाच्या आताच वस्ती करून बसली आहे!
आता आपण एक काम करू. ह्या आकृतीच्या कोणत्याही एका भागात भिंगाने पाहण्याचा प्रयत्न करू. खाली दिलेल्या आकृतीमध्ये एकेका चित्रात त्यातील छोटे भाग हळू-हळू मोठे करून दाखवले आहेत. ते पाहता असे लक्षात येईल की जसे जसे आपण त्या आकृतीच्या आत जात राहू तसे तसे तोच तोच आकार आपल्याला दिसतो आहे. ह्या प्रकाराला 'स्व-साधर्म्य' (self-similarity) असे म्हटले जाते. म्हणजे एखादी आकृती लांबून जशी दिसते, तशीच ती जवळूनही दिसते. तिला कितीही सूक्ष्मतर रुपात पाहत जाऊ, ती तशीच दिसते.
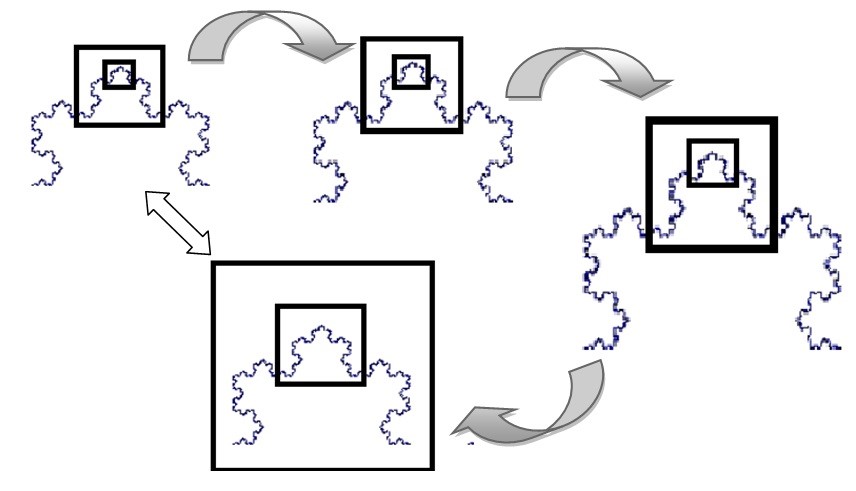
अश्या आकृत्यांमध्ये नागमोडी वळणे आपल्याला लांबून दिसत नाहीत, पण जवळ जाता ते दृष्टिगोचर होतात. जितके त्याच्या आत शिरू तितकी आणखी नागमोडी वळणे दिसायला लागतात. हेच ते कारण ज्यामुळे मँडेलब्रॉट म्हणाला कि समुद्रकिनाऱ्याची लांबी अनंत आहे. (वास्तविक ह्या आत आत शिरण्याला मर्यादा आहेत. कोणती तरी अशी स्थिती येईल ज्यापुढे ह्या रेषेची एकसंधता तुटेल.).
पण यावरून मँडेलब्रॉटच्या असे लक्षात आले की हे स्वसाधर्म्य अनेक गोष्टी विषद करू शकेल. ह्या स्वसाधर्म्याचा गुणधर्म वस्तूंना एका ठराविक छोट्या आकारात सामावून देखील खूप मोठी लांबी देतो. मग याची पुढची पायरी येते ती म्हणजे त्रिमितीमध्ये (3D) ठराविक आकाराच्या आत प्रचंड मोठे क्षेत्र सामावून दाखवणे. एक गंमत म्हणून तुम्ही स्वतः अशी एखादी आकृती काढून पहायचा प्रयत्न करू शकता. किंवा पुढच्या भागाची प्रतीक्षा करा.
या स्वसाधर्म्यामुळे मँडेलब्रॉट जणू काही सगळीकडे तेच पाहू लागला. जळी-स्थळी-काष्ठी-पाषाणी सगळीकडे स्वसाधर्म्य! झाडाच्या पानांत, फुलाच्या पाकळ्यांत इतकेच नाही तर आपल्या शरीरात - रक्तवाहिनींच्या जाळ्यात, फुफ्फुसांच्या जंजाळात - सगळीकडे एक नवीन प्रकारची भूमिती वसते आहे. युक्लीडच्या १, २ किंवा ३ मिती त्या भूमितीला विषद करण्यास अपुऱ्या आहेत. ह्यातूनच 'अपूर्णांक भूमिती (Fractals)' ह्या नवीन भूमितीचा जन्म झाला. ह्या भूमितीने जगाकडे पाहण्याचा एक वेगळाच दृष्टीकोन दिला. लताचे 'आकाश के उस पार भी आकाश है' हे गाणे ऐकताना त्यामागे स्वसाधर्म्य किंवा अपूर्णांक भूमितीच आहे की काय असा मला भास झाला. काय आहे ही भूमिती? पाना-फुलात, रक्तवाहिन्यात तिचा काय उपयोग ? पाहूया पुढच्या भागात.
क्रमशः
(पुढचा भागः जीवनात ही घडी अशीच राहू दे (स्व-साधर्म्य - भाग २))
- शंतनु
मूळ लेख माझ्या स्वतःच्या ब्लॉगवरून पुनःप्रकाशित. हा लेख इतरत्रही प्रकाशित.
Material licensed under a Creative Commons Attribution-NoDerivatives 4.0 International.
(तिसरे रेखाचित्र सोडून सर्व चित्रे विकिपिडीयावरून साभार)

वाह ! मस्त. फार छान माहिती
वाह ! मस्त. फार छान माहिती आहे. अजून वाचायला आवडेल. येऊ द्यात पुढचा लेख.
आहा ! खूप कुतूहल जागवणारा लेख
आहा ! खूप कुतूहल जागवणारा लेख आहे. पुढच्या भागाची प्रतीक्षा करत आहे.
गोंधळ होत चाललाय जितका विचार
गोंधळ होत चाललाय जितका विचार करू तेवढा. पुढचा भाग लवकर यावा.
धन्यवाद मामी, एस, आणि शाली.
धन्यवाद मामी, एस, आणि शाली. पुढचा भाग टाकीन लवकरच.
सही आहे हे! आवडला लेख!
सही आहे हे! आवडला लेख!
(वास्तविक ह्या आत आत शिरण्याला मर्यादा आहेत. कोणती तरी अशी स्थिती येईल ज्यापुढे ह्या रेषेची एकसंधता तुटेल.). >>> याच्याबद्दल अजून माहिती दिलीत तर आवडेल.
बाय द वे, हेच लॉजिक एखाद्या कच्च्या रस्त्याच्या लांबीबद्दलही लागू होउ शकते काय?
अजून एक थोडे अवांतर होईल पण
अजून एक थोडे अवांतर होईल पण मला नेहमी हा प्रश्न पडतो की चौकोन/चौरस्/आयत हे पूर्ण मानवनिर्मीत आकार असावेत. निसर्गात कोणतीच गोष्ट या आकारात दिसत नाही. त्रिकोणही तसाच असेल कदाचित. वर्तुळ, गोल, लंबवर्तुळ, सरळ रेषा हे नैसर्गिक आकार आहेत - वरचे वर्णन वाचून आता "निदान ढोबळ मानाने" असे लिहायला हवे , पण किमान काही गोष्टी (सूर्य, पृथ्वी), किरण हे आपल्याला तसे दिसतात. नैसर्गिक रीत्या चौकोनी दिसणारी कोणतीच गोष्ट नसावी.
, पण किमान काही गोष्टी (सूर्य, पृथ्वी), किरण हे आपल्याला तसे दिसतात. नैसर्गिक रीत्या चौकोनी दिसणारी कोणतीच गोष्ट नसावी.
फा, आमचे काही नॅनोकण त्रिकोणी
फा, आमचे काही नॅनोकण त्रिकोणी असतात. षटकोनीसुद्धा.
फारच उत्कंठा वाढलीये पुढील
फारच उत्कंठा वाढलीये पुढील लेखाची....,
माणसाच्या मेंदूची कमाल आहे.....
षटकोन (स्नो फ्लेक्स,
षटकोन (स्नो फ्लेक्स, मधमाशीचं पोळं) आणि शंकू हे देखिल नैसर्गिक आकार आहेत. शंकू तर अनेक रचनेत दिसून येतो.
लेख आवडला, पुढील भागाच्या
लेख आवडला, पुढील भागाच्या प्रतिक्षेत
उत्कंठावर्धक लेख !
उत्कंठावर्धक लेख !
पुढील भागाच्या प्रतिक्षेत..
मस्त!
मस्त!
पुढील भागाच्या प्रतिक्षेत.
फारएण्ड, चिनूक्स, पुरंदरे
फारएण्ड, चिनूक्स, पुरंदरे शशांक, हर्पेन, मित, आणि रावी, प्रतिसादांबद्दल आभारी आहे.
फारएण्ड, 'रेषेची एकसंधता तुटेल' - हे वाक्य Continuum या संकल्पनेच्या मर्यादेबद्दल आहे. म्हणजे लांबून आपल्याला रेष एकसलग दिसते, पण जवळ जाऊन पहिले तर गोगलगाई साठी एकेक खडा पार करावा लागतो. ते खडेदेखील एकमेकांना चिकटून आहेत असे दिसले तरी आणखी सूक्ष्म पातळीवर जाऊन पाहता ते अणूंचे बनले आहेत आणि त्यांच्या आत मोकळी जागा आहे. म्हणजे प्रोटोन, इलेक्ट्रोन वगैरे एकमेकांना चिकटून नसतील. तिथे ती एकसंधता तुटेल. मग आपल्याला एकसलग रेषेवरून चालत जाऊन अंतर मोजता येणार नाही.
हे लॉजिक कच्च्या रस्त्याच्या लांबीला सुद्धा लागू आहे.
मानवनिर्मित आकार हे कसे निर्माण करण्यात आले, त्यामागची प्रेरणा काय - हा विषय कुतूहलजन्य आहे. तुम्ही 'ढोबळ मानाने' म्हणलात तेच योग्य वाटते, कारण खरे आकार जवळ जाऊन पाहता इतके अचूक वर्तुळ वगैरे नाहीत. कदाचित ढोबळ निरीक्षणावर आधारितच पहिले आकार मानवाने निर्माण केले असावेत.
चिनूक्स, तुम्ही म्हणता त्यात
चिनूक्स, तुम्ही म्हणता त्यात तथ्य आहे. मला नॅनोकण विषयी फार माहिती नाही, पण क्रिस्टल्स सुद्धा ठराविक आकारांचे भासतात - तेही ढोबळ मानानेच असावेत. मामी, स्नो फ्लेक्सचे ही तसेच असेल.
छान लेख शंतनू पुढील भाग लवकर
छान लेख शंतनू पुढील भाग लवकर येऊ देत...
पुढील भाग लवकर येऊ देत...
स्वामी
स्वामी
ही हलकल्लोळ मालिकाच ना ? पुन्हा वाचतानाही तेव्हढंच आवडलं!
हर्षल आणि लीलावती, धन्यवाद
हर्षल आणि लीलावती, धन्यवाद पुढील भाग लिहून तयार, फक्त थोडी डागडूजी बाकी आहे. टाकेन लवकरच!
पुढील भाग लिहून तयार, फक्त थोडी डागडूजी बाकी आहे. टाकेन लवकरच!
लीलावते, हो बरोबर, हलकल्लोळ मालिका
मस्त लेख. सेल्फ सिमिलॅरिटी
मस्त लेख. सेल्फ सिमिलॅरिटी संकल्पना सही आहे.
निसर्गनिर्मित गोष्टीत सिमेट्री असते, पण अशी सेल्फ सिमिलॅरिटी कुठे कुठे दिसते?
झाडाच्या फांद्यात असेल ना? मूळ खोडापासून विभागून फांद्या, मग फांद्याना पुन्हा फांद्या, शेवटी एका दांडीवर अनेक पानं, पानांच्या आत एक शीर, त्यातून अनेक शिरा इ.
अशी मानवी शरीरातील रक्त वाहिन्यात ही असावी, आपली सूर्यमाला आणि अशा अनेक सूर्यमाला त्यातीन अनेक ग्रह, त्यांना असलेले उपग्रह (मून) ही सुद्धा सेल्फ सिमिलॅरिटीच असावी. मस्त संकल्पना आहे.
ह्याला एक डीझाईन पॅटर्न म्हणता येईल का? मानवनिर्मित ठिकाणी मानवाने याचा बराच वापर केलेला दिसतो.
धन्यवाद. तुम्ही विचारलेल्या
धन्यवाद अमितव. तुम्ही विचारलेल्या काही प्रश्नांची उत्तरे जीवनात ही घडी अशीच राहू दे (स्व-साधर्म्य - भाग २) मध्ये आहेत.
ह्याला डिझाईन पॅटर्न म्हणता येईल. तुमचे बरोबर आहे.
बिंदूला मिती नाही पण रेषेला
बिंदूला मिती नाही पण रेषेला मिती आहे यामुळे अनंत परीमिती आणि फायनाइत क्षेत्रफळ हा पाराडोक्स तयार होतो का?
मस्त लेख. पुढचे भाग लवकर येऊ
मस्त लेख. पुढचे भाग लवकर येऊ द्यात
मस्त लेख _/\_
मस्त लेख _/\_
टवणे सर, हा पॅरॅडॉक्स
टवणे सर, हा पॅरॅडॉक्स द्विमितीय आकृतीला अनंत काळ फाटे फोडण्यामुळे निर्माण होतो. येथे बिंदूचा संबंध नाही.
मेधा आणि अॅमी, धन्यवाद.
मेधा आणि अॅमी, धन्यवाद. पुढचा भाग ऑलरेडी टाकला आहे.. - हा पहा: जीवनात ही घडी अशीच राहू दे
हा इतका चांगला माहितीपर लेख
हा इतका चांगला माहितीपर लेख वाचायचा राहून गेला होता.
गणेशोत्सवातल्या रिक्षेसाठी अनेक धन्यवाद.
seems damn interesting. have
seems damn interesting. have bookmarked to read
हा लेख दिसलाच नव्हता, आता वर
हा लेख दिसलाच नव्हता, आता वर आल्यामुळे वाचला. फारच रोचक आहे. दुसरा भाग वाचते. ब्लॉगची लिंक मिळेल का?
धन्यवाद, स्वाती, नानबा, आणि
धन्यवाद, स्वाती, नानबा, आणि वंदना.
वंदना, माझा ब्लॉग इथे मिळेल.
ब्लॉग लिंकसाठी आभार शंतनु.
ब्लॉग लिंकसाठी आभार शंतनु. यावेळी खजिनाच हाती लागलाय, अनपेक्षित अक्षरलाभ योग
रोचक.
रोचक.
Pages